«Квант» для «младших» школьников Задачи 2010 года

«Квант» для «младших» школьников

Задачи первого номера 2010 года

1. По результатам опроса общественного мнения работой президента довольны 76% опрошенных, работой премьера —83%, работой правительства в целом — только 59%. Назовём опрошенного безнадёжным, если он доволен и работой президента, и работой премьера, но недоволен работой правительства в целом. Какая наименьшая возможная доля безнадёжных среди опрошенных?


2. Дан равносторонний треугольник. а) Можно ли разрезать его на равносторонние треугольники двух видов — на большие ималенькие — так, чтобы тех и других было поровну?
а) Можно ли разрезать его на равносторонние треугольники трёх видов — на большие, средние и маленькие — так, чтобы треугольников разных размеров было поровну?

3. Однажды Алиса нашла в Зазеркалье волшебную палочку, которая создаёт любой предмет по желанию Алисы, но только в одном экземпляре. При этом, создав однажды какой-то предмет, волшебная палочка не может в дальнейшем создать такой же предмет вторично. Алисе нужно изготовить 10 одинаковых башмачков для своих путешествий по Зазеркалью. Как ей сделать сделать это с помощью найденной волшебной палочки?
4. Имеется проволока в виде окружности. Как её изогнуть, чтобы при проекции на одну плоскость она давала квадрат, а при проекции на другую плоскость — равносторонний треугольник?
5. Врач сообщил Змею Горынычу, что если Змей будет выкуривать по 6 сигарет в день, то помрёт через 10 лет, а еслипо 17, то через 5 лет. Сколько лет проживёт Змей Горыныч, если бросит курить? (Считаем, что все годы одинаковой длительности, а все сигареты сокращают жизнь на одно и то же время.)

Задачи второго номера 2010 года

1. Число КУБ является кубом. Докажите, что число ШАР кубомне является. (Разные буквы обозначают разные цифры.)

2. Круги радиуса 1 (и, значит, площади π) расположены так, что образовалась изображённая на рисунке кружевная салфетка. Найдите площадь объединения этих кругов.

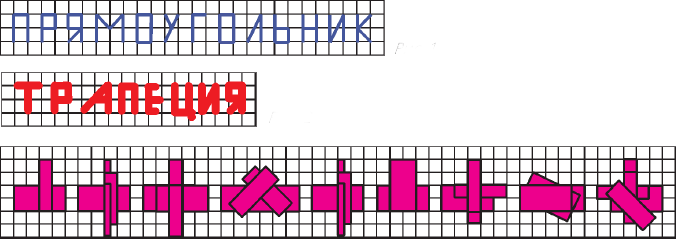
3. Саша взял ручку с тонким пером и красиво, как его учили, по клеточкам написал слово прямоугольник. Артём толстым фломастером написал слово трапеция. Какое слово написала Маша толстым пером?

4. Низкую температуру, нужную для хранения продуктов, люди издавна умели получать без холодильников. Они зимой закладывали в подвалы лёд, а летом размолотый лёд смешивали с солью: температура смеси льда и соли может опуститься до 21 градуса ниже нуля, как в современных морозильных камерах. (Проверьте это на опыте!) А зачем дворники зимой посыпают дорожки солью? Они что, хотят температуру на улице понизить?
5. У мудрого ламы были два ленивых ученика. Как-то лама решил их проучить и предложил сыграть в старинную игру. Они сели за круглый стол, на который высыпали 999 спичек. Ученику, который сел по правую руку от ламы, разрешено за ход брать 1, 3 или 5 спичек. Ученик, который сел по левую руку от ламы, разрешено за ход брать 2, 4 или 6 спичек. Лама, в силу своей мудрости, всегда берёт ровно 1 спичку. Первый ход делает лама, затем ходы делают по очереди по часовой стрелке. Тот, кто не может сделать ход, пропускает его. Выиграет тот, кто возьмёт последнюю спичку. Кто выиграет?

Задачи четвёртого номера 2010 года

1. Барон Мюнхгаузен утверждает, что существуют три натуральных числа a, b, c, обладающие таким свойством: ни a, ни b не делятся на c, но ab делится на c. Не ошибается ли барон?

2. Восемнадцать спичек лежат на плоскости, образуя девятьне перекрывающихсяравносторонних треугольников. Можно ли переложить спички так, чтобы получилось десятьне перекрывающихся равносторонних треугольников (не обязательно одинаковых)?

3. В парке на расстоянии трёх метров друг от друга проходят две параллельные прямые дорожки. Петя и Вася одновременно побежали, каждый по своей дорожке, в одну и ту же сторону. Сначала расстояние между ребятами было три метра, а через минуту стало семь метров. Какое расстояние будет между Петей и Васей ещё через минуту? (Каждый из ребят бежит с постоянной скоростью.)

4. Однажды в мебельном магазине между клиентом (К) и продавцами (П1 и П2) произошёл следующий диалог:
(К) Сколько стоит этот диван?
(П1) 60000 рублей.
(К) Почему так дорого?
(П2) Не удивляйтесь, этот продавец все числа завышает в 3 раза!
(К) Ага, значит, диван стоит гораздо дешевле?
(П1) Это сказал мой напарник? Так ведь он все числа занижает в 12 раз!
Сколько же на самом деле стоит диван, если продавцы, когда называют числа, изменяют их каждый в своё число раз, а в остальном говорят правду?

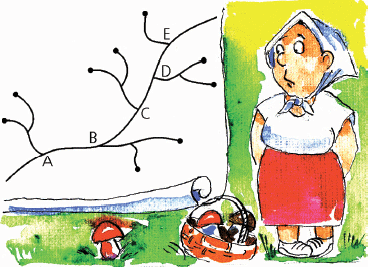5. На плане изображено шоссе, от которого отходят несколько дорог к сёлам. Где на шоссе нужно расположить автобусную остановку, чтобы суммарное расстояние от неё до всех сел (по дорогам и шоссе) было наименьшим?

Задачи пятого номера 2010 года

1. Если КОЕ – ЧТО = 857, на сколькоКТО-ТО больше, чем КОЕ-КТО? (Как обычно, одинаковые буквы обозначают одинаковые цифры, аразные — разные.) 

2. В некотором году количество четвергов равно количеству суббот. Обязательно ли и количество пятниц в этом году такое же? А если год високосный?

3. Я нарисовал многоугольник и провёл в нём все диагонали. Оказалось, что через середину каждой диагонали проходит какая-нибудь другая диагональ,— сказал Петя.
— Это параллелограмм,— сказал Вася.
— Нет.
— Тогда правильный многоугольник.
— Тоже нет.
А вы можете нарисовать такой многоугольник?
4. Зачем машинист длинного товарного поезда, прежде чем тронуться, сдаёт немного назад?

5. На острове живут лжецы (всегда лгут), правдецы (всегда говорят правду) и хитрецы (врут через раз). Однажды встретились три незнакомых между собой мудрых островитянина и между ними произошёл такой разговор:
А: Я не знаю, есть ли среди нас лжецы.
Б: Я не знаю, есть ли среди нас правдецы.
В: Я не знаю, есть ли среди нас хитрецы.
А: Я даже не знаю, есть ли среди вас лжецы.
Б: Я даже не знаю, есть ли среди вас правдецы.
В: Я даже не знаю, есть ли среди вас хитрецы.
Кто из них кто?

Задачи шестого номера 2010 года

1. В фотоателье есть правило: если фотографий меньше ста, то напечатать одну фотографию стоит 3 руб. 50 коп., а если фотографий 100 или больше, то печать одной фотографии стоит 3 руб. Получается, что выгоднее отдать в печать 100 фотографий по 3 руб., чем 99 по 3,5 руб. При каком наименьшем числе фотографий можно добавить ещё несколько фотографий, чтобы после этого плата за печать уменьшилась?

2. Спичками изображена фигура, представляющая собой объединение четырёх одинаковых кубиков. На изображении четвёртый кубик не виден, он спрятан за тремя видимыми кубиками. Переложите девять спичек так, чтобы все четыре кубика этой фигуры можно было увидеть.

Указание

3. Придумайте четырёхзначное число, которое не делится на 2010, но если его запись повторить 15 раз, то полученное многозначное число будет делиться на 2010.

4. Саша, Дима и Федя коллекционируют кусочки пазла «Крошка Енот». Пазл — это картинка, разрезанная на кусочки хитрой формы, среди которых нет одинаковых. Если бы у Феди был жёлтый кусочек с носом Енота, у Саши был зелёный кусочек с хвостом, а у Димы был синий кусочек с лапкой, то любые два мальчика, собравшись вместе, могли бы из своих кусочков составить картинку целиком. Докажите, что уже сейчас втроем мальчики могут целиком составить пазл.

5. Разрежьте по клеточкам квадрат размером 10×10 клеток на 5 прямоугольных частей по схеме, показанной на рисунке, чтобы площадь прямоугольника A была больше площади каждой из остальных частей, и при этом периметр прямоугольника B был больше периметра каждой из остальных частей.