«Квант» для «младших» школьников
Задачи первого номера 1992 года
1. Продав последний персик за 2 рубля 30 копеек, торговец вычислил, что он продавал их в среднем по 2 рубля 45 копеек. Но покупатель вернул ему этот персик, указав на червоточину, и согласился купить его лишь за 1 рубль 58 копеек. Пересчитав среднюю цену, торговец выяснил, что она стала равной 2 рублям 42 копейкам. Сколько персиков продал торговец?
|
2. Завершите заполнение квадрата буквами Т, А, Б, У, Н так, чтобы в каждом горизонтальном, каждом вертикальном рядах и на каждой диагонали присутствовали все эти буквы по одному разу.
Ответ
3. От квадрата отрезан прямоугольный треугольник, сумма длин катетов которого равна длине стороны квадрата. Докажите, что сумма величин углов, под которыми видна из трёх оставшихся вершин его гипотенуза,
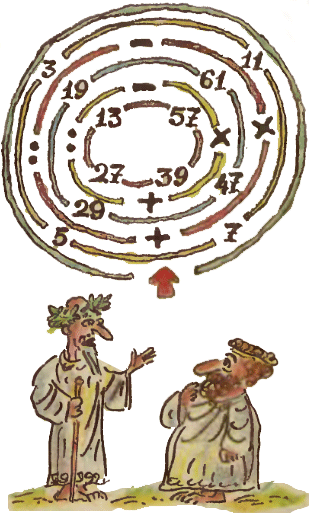4. Пройдите до центра лабиринта так, чтобы в результате получилось число 100.
5. Рассказывают, что некто при встрече с греческим философом и математиком Пифагором спросил его: «Который час?» Пифагор ответил: «До конца суток осталось дважды две пятых того, что уже прошло от начала». Спрашивающийне сразу сообразил, в котором часу произошла встреча. Который был час?
Задачи второго номера 1992 года
1. Когда закончился шахматный турнир, выяснилось, что каждый его участник выиграл белыми фигурами столько же партий, сколько все остальные участники выиграли чёрными. Докажите, что все участники одержали по одинаковому числу побед.
2. В Лондоне над входом в метро висит не буква М, а буква U, поскольку по-английски метро называется underground, что означает «подземка». Это слово начинается и оканчивается одной и той же комбинацией из трёх букв. Найдите русские слова с таким же свойством (содержащие больше 6 букв).
3. Решите арифметический ребус
КИНО · И = ЦИРК.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
4. Маша и Катя вместе весят 40 кг, Катя и Света — 50 кг, Света и Даша — 60 кг, Даша и Галя — 70 кг, Галя и Маша — 80 кг. Сколько весит каждая из девочек?
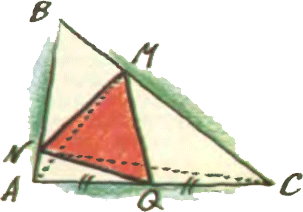5. Величина угла B остроугольного треугольника ABC Задачи третьего номера 1992 года
1. Дед старше внука в 6 раз. Сумма цифр его возраста тоже в 6 раз больше суммы цифр возраста внука, а разности этих цифр равны. Сколько лет внуку?
2. Месяц назад я купил на базаре килограмм картошки, литр молока и десяток яиц. В прошлое воскресенье картошка стала дороже в три раза, молоко — в четыре, яйца — в пять раз, и мне пришлось заплатить за ту же покупку 60 рублей. Сегодня картошка уже стоит в шесть раз дороже, чем месяц назад, молоко — в пять раз, а яйца лишь в четыре раза, и я заплатил за ту же покупку 66 рублей. Сколько денег я уплатил в первый раз?
3. Решите числовой ребус
ДВЕСТИ + ДВЕСТИ + ДВЕСТИ + ДВЕСТИ + ДВЕСТИ = ТЫСЯЧА.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
4. На каждую клетку шахматной доски положили по нескольку монет так, что суммы на каждых двух клетках, имеющих общую сторону, отличаются на одну копейку. На одной из клеток лежат 3 копейки, а на другой — 17 копеек. Какую сумму образуют монеты, лежащие на обеих диагоналях?
5. Даны две концентрические окружности. Проведена хорда большей окружности, касающаяся меньшей. На ней, как на диаметре, построена третья окружность. Докажите, что ограниченная ею площадь равна площади кольца между первоначальными окружностями.Задачи четвёртого номера 1992 года
1. Перед началом урока классный руководитель заметил, что каждый учащийся его класса поздоровался за руку с шестью девочками и восемью мальчиками. Количество рукопожатий между мальчиками и девочками было на пять меньше числа остальных рукопожатий. Сколько учеников в классе?
2. Решите арифметический ребус
ПЧЁЛКА · 7 = ЖЖЖЖЖЖ.
Одинаковым буквам соответствуют одинаковые цифры,разным — разные.
3. Числа 18 и 46 интересны тем, что их квадраты — 324 и 2116 — имеют те же суммы цифр, что и сами числа. Докажите, что обладающих этим свойством натуральных чисел бесконечно много даже среди чисел,не оканчивающихся нулем.
4. Жильцы квартир, выходящих на одну лестничную площадку, решили прикрепить к своим дверям новые номера квартир. Кооператив, в который они обратились с просьбой изготовить необходимые 7 цифр, объявил, что он берёт за изготовление каждой цифры столько рублей, какова эта цифра (например, нули бесплатны). Жильцы собрали по3 рубля с каждой квартиры, и этого им хватило. Какие цифры были заказаны?
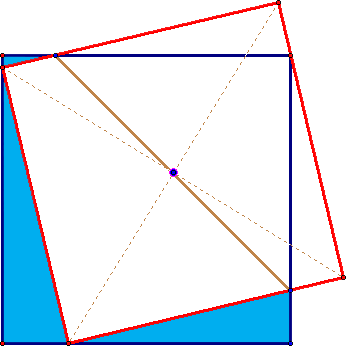5. Два квадрата, синий и красный, расположены так, что две соседние вершины красного квадрата находятся на соседних сторонах синего, а одна из вершин синего квадрата лежит на стороне красного, как показано на рисунке. Докажите, что отрезок, соединяющий другие две общие точки границ этих квадратов, проходит через центр красного квадрата.Задачи пятого номера 1992 года
1. Семь томов энциклопедического словаря стоят в следующем порядке: 1, 5, 6, 2, 4, 3, 7. Расставьте их в порядке возрастания номеров, применив несколько раз следующую операцию: перестановку трёх рядом стоящих томов в начало, в конец или между двумя другими томами, не меняющую порядка этих трёх томов.
2. Решите арифметический ребус-палиндром
ТОРГ · Г = ГРОТ.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
3. Когда я положил в ящик стола связку ключей, то количество ключей в ящике возросло
4. Число 321 составное, но если заменить цифру 2 на цифру 3, получим простое число 331. Найдите наименьшее составное число, которое остаётся составным при произвольной замене любой из цифр.
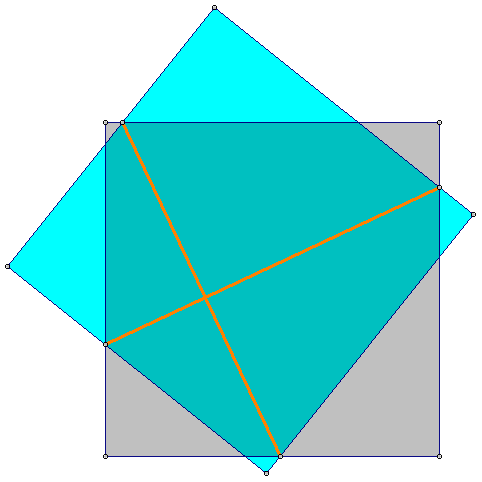
5. Два квадрата в пересечении дают восьмиугольник, как показано на рисунке. Две диагонали этого восьмиугольника делят его на четыре четырёхугольника. Докажите, что эти диагонали перпендикулярны.
Задачи шестого номера 1992 года
1. На балу каждый кавалер танцевал с тремя дамами, а каждая дама — с тремя кавалерами. Докажите, что число кавалеров было равно числу дам.
| |||||||||||||||||||||||||||||||||||||
3. Если обозначить одинаковыми буквами одинаковые цифры, а разными — разные, то во второй половине bd века нашей эры был abed год. Какой это был год?
4. Андрей и Витя купили одинаковые тетрадки, каждая из которых стоила дороже 30 копеек, но дешевле рубля. Андрей платил двадцатикопеечными монетами и получил 3 копейки сдачи, а Витя — пятнадцатикопеечными и одной двухкопеечной монетой. Сколько стоит тетрадь?
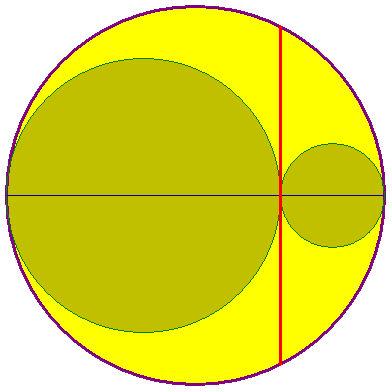5. Длина хорды, касающейся вписанных окружностей, изображённых на рисунке, Задачи седьмого номера 1992 года
1. Укажите все целые числа, которые увеличиваются на 20%, если их цифры записать в обратном порядке.
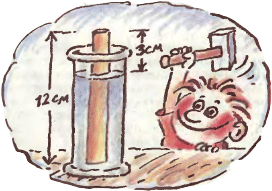2. В мензурке с водой плавает деревянный цилиндр высотой 
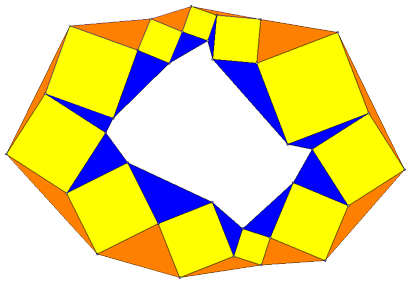3. В цепочке квадратов соединили вершины, как показано на рисунке. Что больше: сумма площадей внешних треугольников или внутренних?
4. Цена на туфли ежемесячно увеличивалась в одно и то же число раз. Полгода назад они стоили
5. В двух кошельках находится по 98 копеек, причём в одном кошельке лежат 49 монет, а в другом — 50 монет. Можно ли уверенно утверждать, что деньги из первого кошелька можно разделить на две равные части? А деньги из второго кошелька?
Задачи восьмого номера 1992 года
1. Мужичок привез продавать на рынок фуки, глюки и друки. Пройдясь по рынку, он решил увеличить запланированные им цены, добавив ещё по одному нулю, но не в концы, а в середины чисел. В результате цена за один фук увеличилась в 6 раз, за глюк — в 7 раз, а за друк — в 9 раз. Сколько они стали стоить, если первоначальная цена каждого из них была меньше 100 рублей?
2. Перед началом международного шахматного турнира в городе Нью-Москва (бывшие Васюки) туда была проведена железная дорога из города Старые Васюки (бывшая Москва) длиной 1993 км. На первом километровом столбе этой дороги написаны числа 1 и 1992, на втором — 2 и 1991, на третьем — 3 и 1990, и так далее. Докажите, что числа на любом из этих столбов взаимно простые.
3. Диаметр AB окружности равен 1. На нём отложен отрезок АС
4. Витя и его младший брат Митя купили по книге. Каждый из них подсчитал сумму цифр всех страниц книги и выяснил, что она равна году его рождения. Как зовут того из братьев, который ходит учиться в школу с математическим уклоном?
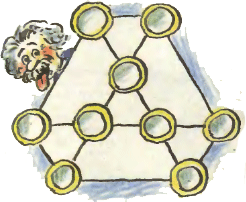5. Расставьте в кружках рисунка цифры 1, 2, 3, ..., 9 так, чтобы суммы чисел в вершинах каждого из семи равносторонних треугольников были равны.Задачи девятого номера 1992 года
1. На свой день рождения фрекен Бок испекла огромный торт. Малыш и торт весили столько же, сколько Карлсон и фрекен Бок. После того, как торт съели, Карлсон весил столько же, сколько фрекен Бок и Малыш. Докажите, что кусок торта, который съел Карлсон, весит столько же, сколько весила фрекен Бок до этого своего дня рождения.
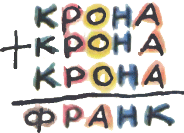2. Расшифруйте арифметический ребус
КРОНА + КРОНА + КРОНА = ФРАНК.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
3. Алёша и Витя начали коллекционировать значки. Хотя у количество значков Вити меньше утроенного числа значков Алёши, но даже в том случае, если Витя отдаст четыре значка Алёше, у него останется больше значков, чем станет у Алёши. Сколько у кого значков, если всего у них меньше двадцати значков?
4. В середине учебного года в классе Стёпы Мошкина сменился милиционер, который вёл занятия по правилам дорожного движения. Дотошный Стёпа выяснил, что год рождения первого милиционера равен сумме номеров страниц «Правил дорожного движения», которые он изучил под его руководством, а год рождения второго милиционера равен сумме номеров оставшихся страниц. На сколько лет один преподаватель старше другого?
5. Лист фанеры размером 10×10 дм распилили на 20 прямоугольников, длины сторон которых измеряются целыми числами дециметров. Сумма длин пропилов равна 100 дм. Докажите, что у каждого из этих прямоугольников есть хотя бы одна сторона длиной 1 дм.
Задачи десятого номера 1992 года
1. Какое наибольшее число полей можно отметить на шахматной доске так, чтобы с любого из них на любое другое отмеченное поле можно было пройти ровно двумя ходами коня?
2. Решите арифметический ребус
ГОЛ2 = ФУТБОЛ.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
3. На плоскости даны две прямые и точка М. Найдите на одной из прямых такуюточку X, что отрезок MX делится другой прямой пополам.
4. В комнате находятся 12 человек. Некоторые из них всегда лгут, а остальные всегда говорят правду. Один из них сказал: «Здесь нет ни одного честного человека», второй: «Здесь не более одного честного человека», третий: «Здесьне более двух честных людей», и так далее вплоть до двенадцатого, который сказал: «Здесь не более одиннадцати честных людей». Сколько в комнате честных людей?
5. Продолжите последовательность чисел: 1, 11, 21, 1112, 3112, 211213, 312213, 212223, 114213, ...
Задачи одиннадцатого номера 1992 года
1. Фома и Ерёма нашли на дороге по пачке семнадцатирублевок. В чайной Фома заплатил без сдачи этими купюрами за четыре стакана чая и семь калачей. Ерёма взял шесть калачей и один стакан чая. Докажите, что и он сможет расплатиться этими купюрами без сдачи. (Стакан чая, как и калач, стоит целое число рублей.)
2. Решите числовой ребус
К · У · КУ = АЛЛО.
Одинаковым буквам соответствуют одинаковые цифры,
3. Парижский метеоролог-любитель, ведший наблюдения с 1897 по 1907 год, делил все дни на холодные, средние и жаркие. Был год, когда число средних дней на столько же превосходило число жарких, на сколько число жарких превосходило число холодных. Назовите этот год.
4. Рассмотрим цепочку из равных касающихся окружностей, центры которых лежат на данной окружности. Что больше: длина данной окружности или сумма длин диаметров окружностей цепочки?
5. Мышка ночью пошла гулять.Кошка ночью видит — мышка!
Мышку кошка пошла поймать.
А вот перевод (построчный) этого стишка на язык племени Ам-Ям:
Ам ту му ям,
Ту ля бу ам,
Гу ля ту ям.
Составьте фрагмент русско-ам-ямского словаря по этому переводу.
Задачи двенадцатого номера 1992 года
1. В вагонах №7, №8, №9 поезда Москва—Сухуми оказались свободные места. Ревизор (любитель математики) отметил, что если поменять местами цифры числа пассажиров вагона №7, то получится число пассажиров вагона №8, а сумма этих чисел равна квадрату числа пассажиров вагона №9. Один из этих трёх вагонов плацкартный, другой — купейный. Какой третий вагон?
2. Найдите два последовательных числа, каждое из которых равно сумме кубов своих цифр.
3. Решите арифметический ребус
ЧЕТЫРЕ + ЧЕТЫРЕ = ВОСЕМЬ.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
4. Если во всех клетках квадрата 4×4 расположить нули, то каждое записанное число будет равно сумме всех своих соседей по горизонтали и вертикали. Можно ли заменить часть нулей (или все) другими числами так, чтобы это свойство сохранилось?
5. Каждую из трёх фигур, изображённых на рисунке, разрежьте на две части, из которых можно сложить квадрат. 
Комментариев нет:
Отправить комментарий