«Квант» для «младших» школьников
Задачи первого номера 1995 года
1. Из книги выпал кусок. Номера первой и последней страниц этого куска являются трёхзначными числами и состоят из цифр 1, 3, 4, но в разном порядке. Сколько страниц содержит выпавший кусок книги?
2. В языке государства Икнатсо всего семь букв: А, И, К, Н, О, С и Т. Всякое слово в этом языке содержит все семь этих букв и является семибуквенным, причём каждый набор из семи различных букв является словом этого языка. Сын короля Икнатсо принц Скоатни издал полный словарь своей страны. Он расположил буквы в алфавите так, чтобы первое слово словаря было «Икнатсо». Сколько слов в словаре? Какое слово будет следовать за словом «Скоатни»? Каким словом завершился словарь?
3. Решите арифметический ребус
КРОСС + КРОСС = СПОРТ.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
4. Двое играют в следующую игру: они по очереди закрашивают клетки на клетчатом поле 4×4. За ход следует закрасить одну клетку так, чтобы не образовалось закрашенного квадрата 2×2. Проигрывает тот, кому не удастся сделать такой ход. Кто выигрывает при правильной игре: начинающий или его партнёр?
5. Существуют ли два многоугольника, у которых все вершины общие, но нет ни одной общей стороны?
Задачи второго номера 1995 года
1. Из фигурок, изображённых на рисунке, сложите равносторонний треугольник.
2. Прекрасная вещь — электронные часы, но ночью разглядеть на них что-либо невозможно. Однажды я выехал поездом Москва—Китеж, отправлявшимся из Москвы в 18 часов. Езды до Китежа 12 часов. И обратный поезд, выходящий из Китежа в 23 часа, тратит на дорогу 12 часов. Я хотел выйти на станции Вешки и старался не уснуть, но уснул и очнулся, когда поезд остановился на какой-то станции. Попытки увидеть время на моих часах не увенчались успехом, но вот я услышал: «К первому пути прибывает поезд Китеж—Москва». После недолгого размышления я вычислил примерное время и успокоился — до Вешек ещё было полчаса езды. А вы сможете вычислить время моего пробуждения?
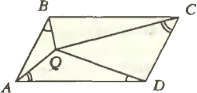3. Внутри параллелограмма ABCD взята точка Q так, что величины углов ABQ и ADQ равны. Докажите равенство величин углов DAQ и DCQ.
4. Существует ли такой четырёхугольник, что любую его вершину можно перенести в новое место, получив четырёхугольник, конгруэнтный исходному?
5. Братья Карамазовы грузили апельсины в бочках. Все бочки были одинаковыми и содержали по Задачи третьего номера 1995 года
1. Какое число стоит на 1995-м месте в последовательности 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, ...?
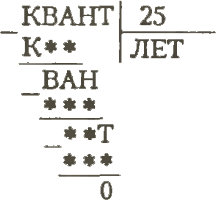2. Замените буквы цифрами так, чтобы равенство стало верным. Одинаковым буквам соответствуют одинаковые цифры,
3. Использовав каждую цифру по одном разу, сложите однозначное, двузначное, трёхзначное и четырёхзначное числа, каждое из которых нацело делится и на 7, и на 9.
4. Какие треугольники можно разрезать на три конгруэнтных треугольника?
5. В прямоугольнике, соответствующем панели кнопочного телефона, «звёздочку и «решётку» заменили некоторыми числами. Кнопки переставили так, чтобы суммы чисел во всех четырёх горизонтальных рядах стали равны и суммы во всех трёх вертикальных рядах тоже стали равны. Какой при этом могла стать наибольшая сумма всех этих чисел, а Задачи четвёртого номера 1995 года
1. Столяр Джузеппе получил заказ на изготовление табуреток. «Если я, начиная с сегодняшнего дня, буду делать по
2. Решите арифметический ребус АБ = БА — замените буквы цифрами так, чтобы равенство стало верным. Одинаковым буквам соответствуют одинаковые цифры,разным — разные.
3. Шли сорок мышей, несли сорок грошей. Две мыши поплоше несли по два гроша. Немало мышей — вообще без грошей. Большие совсем тащили по семь. А остальные несли по четыре. Сколько мышей шли без грошей?
4. Число 19942 + 19942 · 19952 + 19952 является квадратом натурального числа. Докажите это.
5. Может ли предмет, находящийся к северу от наблюдателя, быть южнее его?
Задачи пятого номера 1995 года
1. Из произведения 1 · 2 · 3 · ... · 1994 · 1995 исключили все чётные сомножители и сомножители, делящиеся на 5. Чему равна последняя цифра числа, полученного перемножением оставшихся сомножителей?
2. Те, кто уже принимали быстрорастворимый аспирин «Upsa», наверное обратили внимание, что таблетка аспирина, брошенная в воду, сначала падает на дно, выделяя большое количество пузырьков, но вскоре всплывает, продолжая выделять пузырьки газа. В чём причина всплытия таблетки?
3. Расставьте по кругу четыре единицы, три двойки и три тройки так, чтобы сумма никаких трёх подряд стоящих цифр не делилась на 3.
4. На острове Невезения живут 100 человек. Некоторые из них всегда лгут, а остальные всегда говорят правду. Каждый житель острова поклоняется одному из трёх богов: богу Солнца, Луны или Земли. Каждому жителю острова задали три вопроса:
- Поклоняетесь ли Вы богу Солнца?
- Поклоняетесь ли Вы богу Луны?
- Поклоняетесь ли Вы богу Земли?
На первый вопрос утвердительно ответили 60 человек, на второй — 40 человек, а на третий — 30 человек. Сколько лжецов на острове?
5. Во время семейного шахматного турнира, в котором приняли участие мать, её брат, её сын и дочь, двое игроков были близнецами. Пол близнеца игрока, занявшего последнее место, противоположен полу победителя, а победитель и игрок, занявший последнее место,— лица одинакового возраста. Кто победил в этом турнире?
Задачи шестого номера 1995 года
1. У нас дома есть кусок поролона размерами
2. Решите числовой ребус
СУМК,А + СУМК,А = БАГАЖ.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
3. Из 20 монет достоинства 5, 20 и 50 рублей составьте набор в 500 рублей.
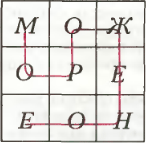4. В квадрате 3×3, изображённом на рисунке, можно прочесть слово МОРОЖЕНОЕ, двигаясь из клетки в клетку через их общую сторону.
5. Ваня Суеверов очень не любит число 13 — «чёртову дюжину»; ему не нравятся не только само число 13 и числа, делящиеся на 13, но и такие двузначные числа, которые станут делиться на 13, если изменить одну из цифр. На крючки с какими номерами предпочитает вешать свою одежду в гардеробе Ваня?
Комментариев нет:
Отправить комментарий