«Квант» для «младших» школьников
Задачи первого номера 1994 года
1. В кошельке лежали купюры в 1, 3, 5 и 10 рублей, причём рублевые купюры составляли половину общей суммы денег. Когда я покупал газету за 16 рублей, ветром унесло 5 купюр. Хватит ли оставшихся на покупку?
2. Проверьте равенства
15 = 1 + 2 + 3 + 4 + 5,
1353 = 13 + 14 + ... + 52 + 53,
133533 = 133 + 134 + ... + 532 + 533,
сформулируйте и докажите общую закономерность.
3. В ночь перед Рождеством Солоха принимает гостей и прячет их в мешки. Если бы она в каждый мешок прятала по одному гостю, то одного мешка не хватило бы. Если бы в каждый мешок она прятала по два гостя, то один мешок остался бы лишним. Сколько человек посадила Солоха в мешки? Примечание. Эта задача скорее по литературе, чем по математике.
4. Решите арифметический ребус
К2 + В2 = А2 + Н2 + Т2
и
К = В + А + Н + Т.
5. Прямоугольник размером 5×9 разрезали на 10 прямоугольников с целыми сторонами. Докажите, что среди них обязательно есть два конгруэнтных.
Задачи второго номера 1994 года
1. Когда у больного удалили зуб, в его верхней челюсти оказалось в 4 раза больше зубов, чем их было в нижней челюсти в прошлом году. Сколько зубов осталось у пациента после операции, если до неё в верхней челюсти было в5 раз больше зубов, чем в нижней?
2. Восстановите пять пропущенных членов последовательности: 102, 105, 111, 114, 120, 123, 129, ?, ?, ?, ?, ?, 201, 204, 210, 213, 219,...3. Решите арифметический ребус
БАРАН + БАРАН + БАРАН + БАРАН = СТАДО.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
4. Капиталист Вова сказал капиталисту Боре: «Если 3/5 моего капитала увеличить на 7 рублей, то получится твой капитал». На это Боря заметил: «Выходит, что у тебя всего на 3 рубля больше, чем у меня». Определите величины их капиталов.
5. Два равнобедренных прямоугольных треугольника приложены друг к другу так, как показано на рисунке. Докажите, что середины сторон образовавшегося невыпуклого четырёхугольника являются вершинами квадрата.Задачи третьего номера 1994 года
1. Баба-Яга и Леший собирали в лесу мухоморы. Оказалось, что крапинок на мухоморах, собранных Бабой-Ягой, в 13 раз больше, чем на мухоморах Лешего. Когда Баба-Яга отдала Лешему свой мухомор с наименьшим числом крапинок, то у неё осталось крапинок лишь в 8 раз больше, чем у Лешего. Докажите, что Баба-Яга собрала не больше 23 мухоморов.
2. Во втором классе учитель вызвал к доске Колю, Васю, Мишу, Стёпу и Гришу и каждому из них задал по примеру из таблицы умножения. Результат каждого последующего умножения оказывался в полтора раза больше предыдущего. Какие числа перемножал Стёпа?
3. Решите арифметический ребус
КУМИР + КУМИР + КУМИР = ШУРИК.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
4. Прямая пересекает треугольник, причём её отрезок внутри треугольника превосходит половину большей стороны треугольника. Докажите, что эта прямая пересекает окружность, вписанную в этот треугольник.
5. Возьмите шестизначное число, которое делится на 7, или на 11, или на 13, или на 37. Переставьте первую его цифру в конец числа. Проверьте, что полученное число вновь делится на то же самое число. Почему?
Задачи четвёртого номера 1994 года
1. По окончании волейбольного турнира, в котором каждая команда встречалась с каждой из остальных по два раза, оказалось, что 20% команд не имели в своём активе ни одной победы (ничьих в волейболе не бывает). Сколько всего встреч было проведено в этом турнире?
2. Число КУБ является кубом целого числа, а число БУК — простое. Какие это числа?
3. «Одна из моих бабушек,— рассказывает Оксана,— старше другой ровно на 1 год, а её муж, мой дедушка, старше второго дедушки тоже ровно на 1 год, но это не самое удивительное. Интересно то, что произведение возрастов дедушек равно четырёхзначному числу, первые две цифры которого составляют возраст моей молодой бабушки, авторые — возраст другой моей бабушки.» Сколько им лет?
4. Замените буквы цифрами так, чтобы равенство
ФАКТ + ФАКТ = НАУКА
стало верным. Одинаковым буквам должны соответствовать одинаковые цифры,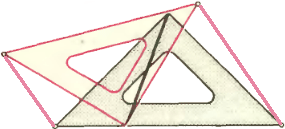 
5. Два чертёжных равнобедренных угольника положили один на другой так, что вершины прямых углов оказались на гипотенузах. Рассмотрим четырёхугольник с вершинами в вершинах острых углов. Докажите, что отрезок, соединяющий прямые углы угольников, делит площадь указанного четырёхугольника пополам.Задачи пятого номера 1994 года
1. Сулико подошла к роднику с двумя кувшинами. Один вмещал 5 литров, а другой — 4 литра. Вода из родника текла двумя струями — одна сильнее, другая слабее. Сулико поставила одновременно кувшины под струи и, когда набралась половина меньшего кувшина, поменяла кувшины местами. Как это ни удивительно, но кувшины наполнились одновременно. Во сколько раз больше воды даёт одна струя, чем другая?
2. Представьте себе огромное число, у которого первая и последняя цифры — единицы, а остальные 1994 цифры — нули. А теперь докажите, что оно — составное.
3. Решите числовые ребусы: УЖ2 = УДАВ, УЖ3 = УДАВ. В каждом из них одинаковым буквам соответствуют одинаковые цифры, а разным — разные. (Одинаковые буквы в разных ребусах могут быть разными).
4. Квадрат размерами 3×3 разбит на единичные клетки. Назовём клетки соседними, если они имеют общую сторону. Попробуйте записать в этих клетках слово МОРОЖЕНОЕ, передвигаясь из клетки в соседнюю клетку так, чтобы в каждом горизонтальном и вертикальном ряду оказалось по одной букве О.
5. Мне вдвое больше лет, чем вам было тогда, когда мне было столько лет, сколько вам теперь. Когда вам будет столько лет, сколько мне теперь, сумма наших возрастов будет равна Задачи шестого номера 1994 года
1. Толя и Серёжа прыгнули с берега в воду и поплыли к острову. Сергей проплыл
2. Решите арифметический ребус КР***УГ = КРУГ2 — замените буквы цифрами так, чтобы равенство оказалось верным. Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
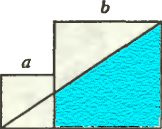3. Два квадрата со сторонами a и b расположены так, как показано на рисунке. Найдите отношение площади заштрихованного четырёхугольника, образованного при соединении двух вершин этих квадратов, к площади большего квадрата.
4. Трое братьев вскапывали огород. После работы их встретил отец.
— Много ли вскопал?— спросил он у старшего брата.
— Один из нас вскопал вдвое больше, чем остальные вместе.
— Не ты ли так поусердствовал?— спросил отец у среднего брата.
— Нет, не я. Вот если бы я вскопал столько же, сколько мои братья вместе, то огород был бы уже вскопан.
— А много ли осталось?— спросил отец у младшего брата.
— Ровно столько, сколько вскопал один из моих братьев,— ответил тот.
Какую часть огорода вскопал каждый из братьев?
— Много ли вскопал?— спросил он у старшего брата.
— Один из нас вскопал вдвое больше, чем остальные вместе.
— Не ты ли так поусердствовал?— спросил отец у среднего брата.
— Нет, не я. Вот если бы я вскопал столько же, сколько мои братья вместе, то огород был бы уже вскопан.
— А много ли осталось?— спросил отец у младшего брата.
— Ровно столько, сколько вскопал один из моих братьев,— ответил тот.
Какую часть огорода вскопал каждый из братьев?
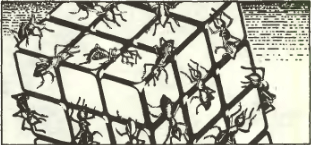5. На каждом из квадратиков «кубика Рубика» сидит по муравью. В некоторый момент все муравьи 
Комментариев нет:
Отправить комментарий