«Квант» для «младших» школьников Задачи 2001 года

«Квант» для «младших» школьников

Задачи первого номера 2001 года

1. У Лёни и Олега были пирожки, которые они поделили пополам. Затем пришёл Коля и принёс ещё 8 пирожков, после чего все пирожки снова поделили поровну. «Теперь мне досталось меньше,— заметил Леня,— но если бы у Коли было на 6 пирожков больше, то мне бы досталось больше пирожков, чем до его прихода». Сколько пирожков досталось каждому?

2. Аня, Маня и Ваня задумали три различных двузначных числа. Каждое из этих чисел делится на сумму квадратов своих цифр. Какие числа задумали Аня, Маня и Ваня?

3. Федерация состоит из 89 субъектов (областей, краёв и т.п.), которые указом Президента объединены в7 федеральных округов. Согласно указу, в каждом округе один субъект является старшим, ему подчиняются два или три средних, а все остальные субъекты — младшие, причём каждому среднему подчиняются два или три младших.В Лесном округе больше субъектов, чем в Болотном, а в Речном — больше, чем в Холмистом. В каком округе субъектов больше — в Снежном или Пустынном?

4. У Пети имеется стеклянный запаянный аквариум в форме прямоугольного параллелепипеда, который не полностью заполнен водой. Петя заметил, что на какую грань аквариум ни ставь, вода всякий раз не достаёт до верха 3 см. Петя предполагает, что аквариум имеет форму куба. Верно ли это предположение?

5. Набор из 20 гирек обладает таким свойством: если произвольным образом по 5 гирек положить на 2 чашкидвухчашечных весов, то оставшиеся 10 гирек можно так разложить по 5 штук на 2 чашки, что весы будут в равновесии. Докажите, что набор можно разложить на 2 группы по 10 гирек так, что в каждой группе массы всех гирек одинаковы.

Задачи второго номера 2001 года

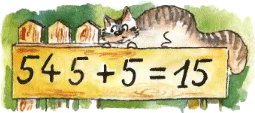1. На доске школьник написал неверное равенство 545 + 5 = 15. Сотрите одну черту, чтобы равенство стало верным. 

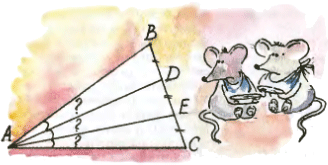2. Точки D и E делят сторону BC треугольника ABC на три равные части. Могут ли при этом лучи AD и АЕ делить угол ВАС на три равных угла? 

3. Папа Карло обнаружил, что длины сторон бруска прямоугольной формы (прямоугольного параллелепипеда) — простые числа. Произведение двух из них на 40 больше третьего, а их разность на 9 меньше третьего. Каков объём бруска?

4. В обрывке старинного манускрипта обнаружена следующая запись:«Наименьший квадрат, из которого можно вырезать любую из этих11 развёрток куба, имеет размеры ...» Проверьте, что каждая из приведённых в манускрипте фигур является развёрткой куба. Найдите размеры наименьшего квадрата, из которого можно вырезать все эти развёртки (за единицу длины примите ребро куба).

5. Известно, что любой дурак считает себя умным, зато всех остальных —дураками. Среди умных могут быть такие, кто считает себя дураком, зато про всех остальных точно знает, кто умный, а кто дурак (как и тот умный, который считает себя умным). Опросы жителей Страны Чудаков позволили точно определить, кто из них умный, а кто дурак. Есть ли в этой стране хоть один умный?

Задачи третьего номера 2001 года

1. Профессор пытался из 8 различных цифр составить число, делящееся на любую из этих цифр. Докажите, что это ему не удалось. Устав от безуспешных попыток составить восьмизначное число, он решил облегчить себе задачу и теперь пытается из 7 различных цифр составить число, делящееся на любую из них. Помогите ему это сделать.

2. Клетки квадрата 100×100 раскрашены в белый и чёрный цвет в шахматном порядке. Квадрат разрезали на квадраты с нечётными сторонами, и в каждом квадрате отметили центральную клетку. Докажите, что белых и чёрных клеток отмечено поровну.

3. Рокер Вася собирается на мотоцикле переехать бордюр, имеющий в сечении форму правильного треугольника с длиной стороны 20 см.
— Радиус каждого колеса моего мотоцикла 30 см,— хвастает Вася. — Переехав этот жалкий бордюр, я оставлю на нём след нулевой длины!
Прав ли Вася?

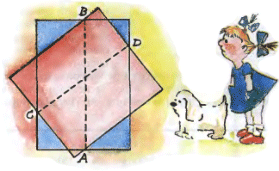4. Два прямоугольника, красный и синий, пересеклись так, что отрезок ABоказался параллельным стороне синего прямоугольника, а отрезок CD —параллельным стороне красного. Докажите, что площади прямоугольников равны. 

5. Один из собеседников сказал:
— Если год, когда мне исполнилось 43 года, умножить на год, когда мне исполнилось45 лет, и поделить на год моего рождения, то получится год, когда...
— Достаточно!— прервал его второй. — Я могу назвать год твоего рождения.
Назовите и вы.

Задачи четвёртого номера 2001 года

1. Дядюшка Скрудж зашёл в магазин спортивных товаров за подарками для племянников. Протянув продавцу 20 долларов, он попросил продать ему один футбольный мяч, три баскетбольных и коробку теннисных. Положена ли ему сдача, если денег на покупку заведомо хватит и один теннисный мяч стоит 33 цента, а одинфутбольный — столько, сколько стоят три волейбольных и пять теннисных мячей вместе?

2. Три весёлых маляра раскрасили рёбра куба в три цвета так, что никакие два одноцветных ребра не имеют общей вершины. Докажите, что рёбер каждого цвета ровно четыре. (Каждое ребро куба окрашено только в один цвет.) 

3. Найдите девять последовательных трёхзначных чисел, обладающих следующим свойством: если в каждом из этих чисел перемножить цифры, а затем сложить полученные девять произведений, то в результате получится число 1125.

4. На плоскости расположены два конгруэнтных, но несовпадающих треугольника. Одна прямая делит площадь каждого из них пополам, а вторая прямая делит пополам их периметры. Могут ли эти две прямые быть перпендикулярны?

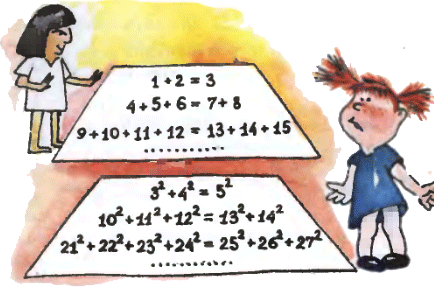5. Найдите и обоснуйте закономерности, которым подчиняются числовые равенства, написанные в пирамидах.

Задачи пятого номера 2001 года

1. Вдоль аллеи стоят 20 столбиков, каждый из которых имеет высоту 1 м, 2 мили 3 м. Вася, идя в одну сторону, насчитал 13 пар соседних столбиков, высота столбиков в которых возрастала. Когда он шёл обратно, то насчитал 5 такихпар. Не ошибся ли Вася в расчётах?

2. Какие простые числа представимы в виде разности двух чисел, десятичная запись первого из которых состоит из b цифр a, а второе состоит из a цифр b?

3. Средняя температура врачей больницы отличается от средней температуры больных, но среднее этих двух чисел совпадает со средней температурой всех врачей и больных этой больницы. Кого в больнице больше, врачей или больных? 

4. Некоторые из 50 ребят знают все буквы, кроме «р», которую они пропускают при письме, а остальные знают все буквы, кроме «к» (и пропускают её при письме). Однажды учитель попросил 10 учеников написать слово «кот», 22 других учеников —слово «крот», а остальных 18 — «рот». При этом слова «кот» и «рот» оказались написанными по 15 раз. Сколько ребят написали своё слово верно?

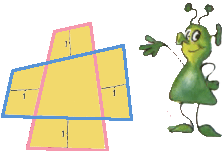5. У крестообразно пересекающихся четырёхугольников соответственные стороны параллельны и отстоят друг от друга на расстояние 1. Докажите, что периметры четырёхугольников равны



.

Задачи шестого номера 2001 года

1. В корзине лежат 13 яблок. Имеются весы, с помощью которых можно узнать сумму масс любых двух яблок. Придумайте способ выяснить за 8 взвешиваний суммарную массу всех яблок.

2. На кошачьей выставке в ряд сидят 10 котов и 19 кошек, причём рядом с любой кошкой сидит хотя бы один более толстый кот. Докажите, что рядом с любым котом сидит хотя бы одна более тонкая кошка. 

3. На кольцевой автотрассе расположены три посёлка А, B, C. Где нужно расположитьпочту P, чтобы сумма длин линий связи, соединяющих почту с тремя посёлками (сумма длин хорд PА, PB и PC) была наименьшей?

4. Выпуклый шестиугольник ABCFGH таков, что АВ = CF = GH, углы A, C, G равны, как равны между собой и углы B, F и H. Докажите равенства BC = FG = НА.

5. Играя в домино, Баба, Табриз, Гамид и Эльмир взяли кости с различной суммой очков. Сумма очков у Бабы и Табриза оказалась равной сумме очков у Гамида и Эльмира, а разница очков Бабы и Табриза оказалась в 3 целых 6 седьмых раза больше разницы очков Гамида и Эльмира. Назовите 12 костей домино, которые находятся на руках у Бабы и Табриза.