«Квант» для «младших» школьников Задачи 1998 года

«Квант» для «младших» школьников

Задачи первого номера 1998 года

1. Пешеход, велосипедист и мотоциклист едут по одной дороге в одинаковом направлении. В некоторый момент мотоциклист оказался в 100 метрах от велосипедиста и 400 метрах от пешехода. Через 6 минут мотоциклист обогнал велосипедиста и ещё через 6 минут обогнал пешехода. Когда велосипедист обгонит пешехода, если все они движутся с постоянными скоростями?

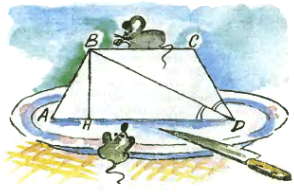2. ВН — высота равнобочной трапеции ABCD. Диагональ DB — биссектриса углаADC. Докажите, что величина угла HBD равна сумме величин углов ABH и CBD.

3. Шахматный король обошёл по одному разу все поля шахматной доски и последним ходом вернулся в начальное положение. Докажите, что он при этом сделал чётное число ходов по диагонали.

4. Из 15 школ района отобрали 100 учащихся для участия в математической олимпиаде. Покажите, что хотя бы из двух школ было отобрано одинаковое количество участников (может быть ни одного).

5. У одной из фирм имеется несколько филиалов и несколько представительств. В каждом филиале установлено по5 компьютеров, а в каждом представительстве — лишь по 2 компьютера, но зато имеется 7 сотовых телефонов. Общее количество компьютеров на столько же превосходит общее количество сотовых телефонов, на сколько процентов число филиалов больше числа представительств. Сколько у фирмы представительств?

Задачи второго номера 1998 года

1. Восьмиклассники построены в шеренгу. Перед каждым из них стоит семиклассник, который ниже его ростом. Докажите, что если шеренги семиклассников и восьмиклассников построить по росту, то по-прежнему каждый восьмиклассник будет выше стоящего перед ним семиклассника.

2. Мастер спорта Седов, кандидат в мастера Чернов и перворазрядник Рыжов встретились в клубе перед началом турнира.
— Обратите внимание,— заметил черноволосый,— один из нас седой, другой рыжий, а третий черноволосый. Но ни у кого цвет волос не соответствует фамилии. Забавно, не правда ли?
— Ты прав,— подтвердил мастер.
Какого цвета волосы у кандидата в мастера?

3. Десять человек пришли в гости в галошах. Уходили они по одному, и каждый надевал произвольную пару галош, в которую он мог влезть (то есть не меньшего размера, чем его собственная). Какое наибольшее число людейне смогло надеть галоши?

4. Из спичек сложено слово «ТОЛЯ». Переложите одну спичку так, чтобы получилось женское имя.

5. На каждой горизонтали и каждой вертикали шахматной доски стоит нечётное число фигур. Докажите, что на чёрных клетках шахматной доски стоит чётное число фигур.

Задачи третьего номера 1998 года

1. У Серёжиной мамы три сына. Первого она назвала Андреем. Второго — Борисом. Как зовут её третьего сына?

Ответ

2. Когда канатоходец встал на середину каната, натянутого между двумя столбами, то канат удлинился на 40 см, а артист опустился на 1 м. Какова была первоначальная длина каната?

3. Решите систему уравнений 7562x + 2438y = 47 562 и 2438x + 7562y = 42 438,
 не прибегая к помощи карандаша и бумаги.

Ответ   Указание   Решение

4. В турпоход отправились 9 юношей и 10 девушек. На привале один из них заметил, что до похода каждый юноша был знаком с одинаковым числом девушек, идущих в поход, а все девушки были знакомы с разным количеством юношей. Могло ли такое быть?

Ответ   Указание   Решение

5. В городе Старозаводске троллейбус связывает центр города с заводом. Поэтому в субботу и воскресенье на нём практически никто не ездит. В связи с этим городская Дума постановила, что цена декадного проездного билета должна быть пропорциональна количеству рабочих дней в декаде. В один из месяцев стоимость всех трёх декадных проездных билетов оказалась одинаковой, причём в этом месяце не было праздничных дней. Назовите эти месяц и год.

Ответ   Решение

Задачи четвёртого номера 1998 года

1. На доске написано несколько различных целых чисел, причём сумма любых двух из них также написана на доске. Сколько чисел написано?

2. Когда в день рождения одного из членов редколлегии спросили, сколько ему исполнилось лет, он ответил, что если к году его рождения прибавить текущий год, затем вычесть год, когда ему исполнилось 20 лет, и вычесть год, когда ему исполнилось 30 лет, то в результате получится 16. Сколько же лет ему исполнилось?

3. Можно ли доску для игры в шашки распилить на нечётное число прямоугольников таким образом, чтобы все распилы шли по границам клеток, а количества чёрных клеток, попавших в эти прямоугольники, составляли возрастающую арифметическую прогрессию?

Ответ

4. Из школьного учебника по математике взяли пример и все цифры заменили звёздочками: *^* = **. Расшифруйте этот ребус, зная, что все цифры — чётные.

Ответ

5. Клетки доски размером 11×11 закрашены в шахматном порядке так, что белых клеток на доске на одну больше, чем чёрных. На чёрных клетках доски расставлены 11 ладей. Докажите, что среди них найдутся две ладьи, которые бьют друг друга.

Ответ

Задачи пятого номера 1998 года

1. Радиус переднего колеса едущего трактора равен 25 см. За секунду оно совершает 2,5 оборота. Диаметр заднего колеса равен 125 см. Сколько оборотов оно делает за одну секунду?

Ответ

2. В футбольном турнире между четырьмя командами 7-х классов победилакоманда 7«А», выигравшая все три матча с общим счётом 7 : 1. Команда 7«Г»проиграла все матчи с общим счётом 1 : 6. Команды 7«Б» и 7«В» по одной игре выиграли, по одной проиграли и по одной сыграли вничью. Общий счёт у команды 7«Б» — 2 : 3, а у 7«В» — 3 : 3.Команда 7«А» выиграла у команды 7«Б» со счётом 3 : 0. Как окончились остальные матчи?

3. Внутри тупого угла АОВ проведены лучи ОС, OD и ОЕ, причём луч OC перпендикулярен лучу OA, OD — биссектриса угла АОВ, а OE — биссектриса угла ВОС. Чему равна величина угла DOE?

4. На прямой расположены 100 гирек. Массы любых двух соседних гирек отличаются ровно на 1 г. Докажите, что эти гирьки можно разложить по 50 штук на чашки весов так, что весы окажутся в равновесии.

5. Шесть волейбольных команд решили провести турнир в один круг так, чтобы каждая команда ежедневно играла одну игру. Первые три дня команды играли, выбирая партнеров случайным образом, но с условием, что все три дня они играют с разными командами. Сможет ли появившийся судья турнира составить расписание на оставшиеся два дня так, чтобы все команды сыграли со всеми ровно по одному разу?

Ответ   Указание   Решение

Задачи шестого номера 1998 года

1. Буратино хочет купить букварь, но ему не хватает 18 сольдо. На этот же букварь Мальвине не хватает 7 сольдо, аПьеро — 10 сольдо. Могут ли Пьеро и Мальвина вместе купить один букварь на двоих?

Ответ   Решение

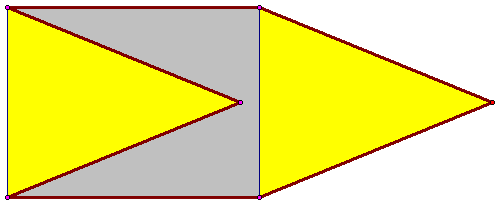2. На рисунке показано, как прямоугольник можно разрезать на две части и сложить из них невыпуклый равносторонний шестиугольник. Можно ли разрезать произвольный прямоугольник на три части и сложить из них выпуклый равносторонний шестиугольник?

3. Любое ли чётное натуральное число представимо в виде суммы двух натуральных слагаемых, каждое из которых состоит из нечётных цифр?

Ответ   Указание I   Указание II

4. Три трёхзначных числа, в записи которых участвуют все цифры, кроме нуля, дают в сумме 1665. В каждом числе первую цифру поменяли местами с последней — получили три новых трёхзначных числа. Чему равна сумма полученных чисел?

5. Король обошёл все поля шахматной доски, побывав на каждом по одному разу. Когда соединили центры полей, по которым он последовательно прошёл, получилась ломаная без самопересечений. Найдите наибольшее возможное число диагональных ходов в маршруте короля.