«Квант» для «младших» школьников Задачи 1986 года

«Квант» для «младших» школьников

Задачи первого номера 1986 года

1. Однажды я решил проехаться по кресельной канатной дороге. В некоторый момент я обратил внимание, что едущее мне навстречу кресло имеет номер 95, следующее —номер 0, а дальше 1, 2 и так далее. Я взглянул на номер своего кресла. Он оказалсяравным 66. Проехал ли я половину пути? При встрече с каким креслом я проеду половину пути?

Ответ   Решение

2. Вот очень простая

Г + О = Л – О = В · О = Л – О = М – К = А.

Замените буквы цифрами так, чтобы получились верные равенства; одинаковым буквам соответствуют одинаковые цифры, а разным — разные.

Ответ

3. Во флакон неправильной формы налили некоторое количество жидкости. Не используяникаких измерительных инструментов и других сосудов, научитесь узнавать, занимает жидкость больше или меньше половины объёма флакона.

Ответ

4. Найдите центр нарисованной окружности, имея в своём распоряжении лишь карандаш и линейку с параллельными краями (ширина линейки меньше диаметра окружности).

5. Дедушка с тремя внуками вышел прогуляться в парк. Встретившийся им дедушкин знакомый спросил, сколько каждому из них лет. Ваня сказал: «Я младше Пети; мне больше пяти лет». Петя произнёс: «Я младше Саши на 3 года». А Саша сказал: «Нам всем вместе в 3 раза меньше лет, чем дедушке, а вместе с дедушкой нам ровно 100 лет». Сколько лет каждому из внуков?

Ответ   Решение

Задачи второго номера 1986 года

1. В этом году я отпраздновал свой день рождения. Число исполнившихся мне лет во многом примечательно.

• Если от этого числа отнять 2, то оно разделится на 3, а если от него отнять 3, то оно разделится на 2.
• Если к нему прибавить 4, то оно разделится на 5, а если от него отнять 5, то оно разделится на 4.
• Если от него отнять 5, то оно разделится на 6, а если от него отнять 6, то оно разделитсяна 5.
• Если к нему прибавить 7, то оно разделится на 8, а если к нему прибавить 8, то оно разделится на 7.

Сколько же лет мне исполнилось?

Ответ

2. Замените буквы цифрами так, чтобы выполнялись равенства

(ОН)³ = ВАНЯ и В + А + Н + Я = ОН

(одинаковым буквам соответствуют одинаковые цифры, а разным — разные).

Ответ

3. Дым, который мы видим,— это мелкие частицы несгоревшего топлива. Их плотность во много раз больше плотности воздуха. Почему же эти частицы поднимаются вверх?

Ответ

4. На днях я жарил оладьи. Когда я начал переворачивать одну из них, она никакне входила на старое место. Оладьи удалось вновь разместить на сковороде, лишь перевернув их все.
Докажите, что всегда можно уложить перевернутые оладьи на круглой сковороде, на которой они лежали раньше, и приведите пример, в котором нельзя ни одну из оладий, перевернув, уложить на старое место.

Указание

5. Разрежьте каждую из двух маленьких фигур одинаковым образом на четыре части так, чтобы из полученных восьми частей можно было сложить вдвое большую (по площади) подобную фигуру.

Задачи третьего номера 1986 года

1. Руслан купил для своей коллекции четыре марки: кубинскую, монгольскую, болгарскую и польскую. Стоимость покупки без кубинской марки — 40 копеек, без монгольской — 45 копеек, без болгарской — 44 копейки, а безпольской — 27 копеек. Сколько стоит каждая марка?

Ответ   Указание

2. Если к двадцати прибавить шестнадцать, получится 36 — полный квадрат. Если от двадцати отнять шестнадцать, получится четыре — тоже полный квадрат. Существуют ли ещё числа, которые становятся полными квадратами после прибавления и вычитания числа 16?

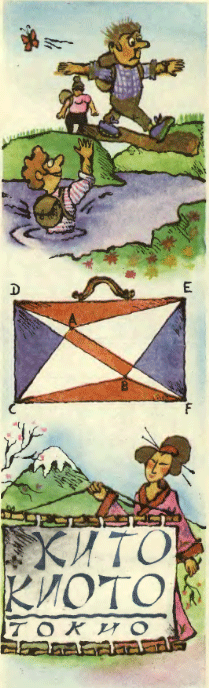3. Туристы подошли к небольшой речке, через которую переброшено бревно. Им нужно перебраться на другую сторону. Первый турист пошёл по бревну и упал в воду, но сумел перебраться на другой берег вплавь. Тогда руководитель быстро перебежал по бревну. За ним перебежали на другую сторону и остальные туристы. Почему по бревну лучше перебежать, чем перейти?

Указание

4. Точки A и B, взятые внутри прямоугольника CDEF, соединили с его вершинами. Два из образовавшихся треугольников закрасили в синий цвет, ещё два — в красный цвет, так же как и центральный четырёхугольник. Докажите, что площадь красной части прямоугольника равна площади его синей части для любого расположения точек A и Bвнутри прямоугольника.

Указание   Решение

5. При каком основании системы счисления имеет решение (и какое) числовой ребус

КИТО + КИОТО = ТОКИО?

Ответ   Указание

Задачи четвёртого номера 1986 года

1. Весёлый турист пешком отправился на слёт. В первый день пути он прошёл ¹/₃ пути, во второй день он прошёл ¹/₃ остатка, в третий день турист прошёл ¹/₃ нового остатка. В результатетуристу осталось пройти 32 км. Сколько километров от дома туриста до места слёта?

2. В шестом номере журнала «Квант» в «Задачнике «Кванта»» будут опубликованы задачи по математике с номерами от М986 до М990. У первой из них номер совпадает с последними тремя цифрами года выхода журнала. А в каком номере журнала номер задачи по математике совпадёт полностью с номером года? (Предполагается, что в каждом номере по-прежнему будет печататься по пять задач по математике и что журнал будет выходить ежемесячно.)

3. Пожарив на сковороде яичницу, я взялся за ручку, чтобы поставить сковороду на стол, но она была очень горячая. Я обернул ручку тряпочкой; но всё равно было горячо. Тогда я намочил тряпочку водой. Что я почувствую на этот раз?

4. Пакет для молока склеивается из цилиндрического бумажного кольца. (Получается треугольная пирамида. Для удобства транспортировки грани пирамиды обычно являются равнобедренными, но не равносторонними треугольниками.) Предположим, что из бумаги склеен пакет, у которого все грани —правильные треугольники. Разрежьте его в цилиндрическое кольцо, высота которого равна половине длины рёбра пирамиды.

5. Расшифруйте числовые ребусы, изображённые на рисунке.

Задачи пятого номера 1986 года

1. У Пети три брата. Первый старше его на три года, второй моложе его на три года, третий моложе Пети втрое. Зато отец втрое старше Пети. Всем вместе им 95 лет. Сколько лет каждому?

2. Решите числовой ребус

USA + USSR = PEACE.

Одинаковым буквам соответствуют одинаковые цифры, разным — разные.

3. Наша речка небольшая. Обычно я перехожу её, погружаясь не более чем по пояс. Дно илистое, и ноги проваливаются в ил по щиколотку. Однажды после сильных дождей вода в реке сильно поднялась. Теперь уже, переходя реку, я опускался в воду по шею. Интересно, что при этом ноги перестали вязнуть в иле. Почему?

Решение

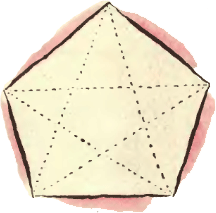4. Пятиугольник разрезан на 11 частей. Расставьте в них числа 1, 2, ..., 11 так, чтобы суммы чисел были равны во всех треугольниках, все вершины которых являются вершинами пятиугольника.

5. На столе лежат три красные палочки разной длины, причём сумма длин равна 30 см, и пять синих палочек, сумма длин которых тоже равна 30 см. Можно ли распилить те и другие палочки так, чтобы их потом можно было расположить парами, и в каждой паре длины палочек были одинаковы, а цвета разные?

Задачи шестого номера 1986 года

1. Определите величину угла, который стрелки часов составляют в 9 часов 20 минут.

2.Расшифруйте числовой ребус

КТО + КОТ = ТОК. 

3. В те, ещё не столь давние времена, когда непременной принадлежностью чаепития был пыхтящий самовар с восседающим на нём заварным чайником, накрытым расшитой льняной салфеткой, заварные чайники делались с дырочкой в крышке (такие чайники делают и сейчас). Зачем нужна такая дырочка?

4. Найдите наименьшее число, сумма цифр которого делится на 17, и сумма цифр следующего за ним числа тоже делится на 17.

5. Алик, Боря, Витя и Гена ходили по грибы. Алик с Борей вместе собрали грибов столько же, сколько Витя с Геной вместе, а у Алика с Геной грибов оказалось меньше, чем у Бори с Витей. Гена нашёл грибов больше, чем Витя. Расположите имена мальчиков в порядке убывания количеств найденных грибов.

Задачи седьмого номера 1986 года

1. Решите в целых числах уравнение

xy + 3x – 5y = –3.

2. Все точки некоторой окружности произвольным образом окрашены в два цвета. Докажите, что существует равнобедренный треугольник с одноцветными вершинами, вписанный в эту окружность.

3. К сумме цифр двузначного числа aприбавили квадрат этой суммы и получиличисло a. Найдите a.

4. CM — медиана треугольника ABC. Сумма величин угловCAB и MCB равна 90°.Докажите, что треугольник ABC —прямоугольный или равнобедренный.

5. На окружности радиуса 10 расположены несколько непересекающихся дуг общей длины 32. Докажите, что для любой прямой существует хорда окружности, параллельная этой прямой, концы которой принадлежат двум таким дугам.

Задачи восьмого номера 1986 года

1. Белых грибов я после дождя набрал — насилу дотащил,— рассказывал на уроке математики Николай Борисович. — Но тащил я главным образом воду: ведь в свежесобранных грибах 90% воды! А когда грибы подсохли, их вес уменьшился на15 кг, потому что вода составляла теперь только 60% их веса. Сколько килограммов грибов я принёс из леса?

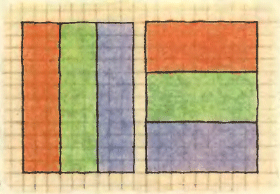2. На рисунке изображены два прямоугольника 9×12, раскрашенные по-разному в три цвета. Разрежьте прямоугольник, нарисованный слева, на 4 части так, чтобы из них можно было сложить прямоугольник, нарисованный справа.

3. Коля и Витя живут в одном доме. На каждом из этажей во всех подъездах их дома расположено по четыре квартиры. Коля живёт на пятом этаже в квартире номер 83, а Витя — на третьем этаже в квартире номер 169. Сколько этажей в их доме?

4. Мы с Ирой пошли в лес за ягодами. Ира шла правее меня. Вдруг слева я услышал её «Ау!», через минуту — снова «Ау!», но уже, кажется, сзади. Почему в лесу так трудно определить направление на источник звука?

5. На стол положили несколько одинаковых листов бумаги прямоугольной формы. Верхний лист покрывает больше половины площади каждого из остальных листов. Можно ли воткнуть булавку так, чтобы она проколола все листы?

Задачи девятого номера 1986 года

1. Был уже вечер, покупатели разошлись по домам, а до конца работы у Наташи —продавщицы овощногомагазина —оставалось ещё полчаса. На прилавке лежали три кочана капусты, два арбуза, дыня и свёкла. Чтобы скоротать время, Наташа стала взвешивать эти овощи и с удивлением обнаружила, что все три кочана капусты весят одинаково, и у обоих арбузов равный вес. Более удивительным было равновесие ещё в трёх случаях, изображённых на рисунках. Теперь ответьте: во сколько раз дыня тяжелее свёклы? 

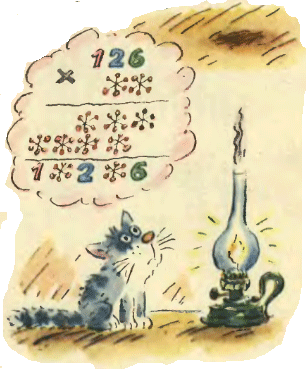2. Восстановите цифры, заменённые звёздочками.

3. Предшественница электрической лампочки — керосиновая лампа —временами коптила, поэтому над ней на потолке образовывалось чёрное пятно. Но и над светильниками с электрическими лампочками иногда возникает тёмное пятно на потолке. Неужели и электрические лампы коптят?

4. При каком наименьшем количестве монет можно уплатить без сдачи любую сумму от 1 копейки до 100 копеек? (Монеты в 1986 году были следующих достоинств: 1, 2, 3, 5, 10, 15, 20, 50 копеек.)

5. В момент, когда мы выключаем газ под кипящим чайником, из-под его крышки вырываются клубы пара. Почему?

Задачи десятого номера 1986 года

1. Как в треугольнике ABCпровести ломануюBDEFG, чтобы площади всех пяти полученных треугольников были равны?

2. Произведение миллиарда натуральных чисел равно миллиарду. Какое наибольшее значение может принять сумма всех этих чисел?

3. Можно ли к числу 9999 приписать справа ещё четыре цифры так, чтобы полученное восьмизначное число оказалось квадратом целого числа?

4. Два одинаковых чайника с водой одинаковой температуры поставили на одинаковые источники тепла. Через некоторое время вода в обоих чайниках закипела, как показано на рисунках. В каком чайнике вода закипела раньше?

5. Винни-Пух и Пятачок одновременно отправились в гости друг к другу. Но поскольку Винни-Пух всю дорогу сочинял очередную «шумелку», а Пятачок считал пролетавших галок, они не заметили друг друга при встрече. После встречи Пятачок подошёл к дому Винни-Пуха через четыре минуты, а Винни-Пух подошёл к дому Пятачка через одну минуту. Сколько минут был в пути каждый из них?

Задачи одиннадцатого номера 1986 года

1. Разрежьте фигуру, изображённую на рисунке, на три конгруэнтные части.

Ответ

2. Железнодорожные рельсы закрепляют на шпалах для того, чтобы рельсы не сдвигались в сторону. Какую ещё важную роль играют шпалы?

Ответ

3. В записи *** + ** = *** замените звёздочки цифрами так, чтобы равенство имело смысл и было правильным после поворачивания листа бумаги, на котором оно записано,на 180°.

Ответ

4. У продавца, который привёз на базар продавать орехи, оказались неправильные рычажные весы и правильная килограммовая гиря. Чтобы отвесить покупателю 2 кгорехов, он один раз уравновесил гирю орехами, положив её на правую чашку весов, а другой раз уравновесил эту гирю орехами, положив её на левую чашку весов. Оказалось, что в результате он отвесил больше 2 кг орехов (докажите это!). Как продавец мог отвесить ровно 2 кг орехов?

Указание I   Указание II   Указание III

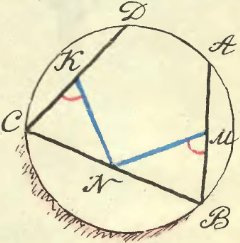5. В круге провели хорды АВ, ВС и CD и отметили их середины M, N и K соответственно. Докажите равенство величин углов BMN и NKC.

Указание I   Указание II   Решение

Задачи двенадцатого номера 1986 года

1. Проверьте равенство

(3² + 5²)² = 16² + 30²

и докажите, что квадрат суммы двух квадратов различных целых чисел обязательно является суммой двух квадратов целых чисел.

Ответ

2. Решите арифметический ребус

НИТКА + НИТКА = ТКАНЬ.

Одинаковым буквам соответствуют одинаковые цифры, разным — разные.

Ответ

3. Заядлый альпинист дядя Серёжа рассказал нам, что сумерки в горах заметно короче, чем на равнине. Как вы думаете, с чем это связано?

Решение

4. Чтобы попасть домой из Дворца пионеров, я могу выйти либо на станции метро «Математическая», либо на следующей — на станции «Физическая». От станции «Математическая» я иду втрое дольше до дома, чем от станции «Физическая», причём пока поезд подходит к станции «Физическая», я успеваю пройти треть пути от станции «Математическая» до дома. В каком случае я быстрее попаду домой?

Ответ

5. На рисунке изображена часть крепостной стены. Один из камней стены имеет столь причудливую форму, что если вытащить его из стены и положить иначе, то стена станет ровной. Нарисуйте такой камень!

Решение