«Квант» для «младших» школьников Задачи 1990 года

«Квант» для «младших» школьников

Задачи первого номера 1990 года

1. Если человек, стоявший в очереди перед вами, был выше человека, стоявшего после того человека, который стоял перед вами, то был ли человек, стоявший перед вами, выше вас? 

2. У окна стоят четыре девочки. Каких девочек достаточно попросить повернуться, чтобы выяснить, истинно ли такое утверждение: «Если девочка без очков, то у неё в волосах бантик»?

3. Найдите два натуральных числа, разность и частное которых — одно и то же целое число.

К О Р А Н О Р К А

4. Заполните пустые клетки квадрата буквами К, О, Р, А и Н так, чтобы в каждом горизонтальном и вертикальном ряду, а также по диагонали, идущей из левой нижней клетки в правую верхнюю, все буквы были различны.

Указание   Ответ

5. Сколько оборотов в сутки делает биссектриса между часовой и минутной стрелками?

Задачи второго номера 1990 года

1. На дерево села стая птиц — на каждую ветку по три птицы,— а одна птица продолжала летать вокруг дерева. Потом все птицы пересели на дерево по четыре на ветке, при этом одна ветка осталась свободной. Сколько было птиц и сколько веток?

2. В одной из новогодних телепередач поэт А. Вознесенский прочитал своё стихотворение, в котором утверждалось, что шоферы считают счастливыми те номера машин, в которых сумма цифр первой половины номера равняется сумме цифр второй половины. Номер 1982 — счастливый, так как1 + 9 = 8 + 2. А в одной из передач серии «Следствие ведут знатоки» утверждалось, что по шофёрскому поверью счастливым является номер, в котором сумма чисел первой и второй половины равняется 100, например 1981, так как 19 + 81 = 100. Перечислите все номера, счастливые одновременно в первом и во втором смысле.

3. Число БАОБАБ делится на 101. Какое это число?

4. Из последовательности всех простых чисел 2, 3, 5, 7, ... построили две другие последовательности: 5 = 2 + 3,8 = 3 + 5, 12 = 5 + 7, ... и 6 = 2 · 3, 15 = 3 · 5, 35 = 5 · 7, ... В первом случае складываются последовательные простые числа, а во втором — они перемножаются. Может ли какой-нибудь член первой последовательности равняться некоторому члену второй последовательности?

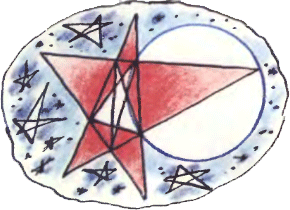5. Существует ли пятиугольная звёздочка с таким свойством: вокруг любого её красного четырёхугольника (смотрите рисунок) можно описать окружность?

Задачи третьего номера 1990 года

1. Из A в B вышел путник. Одновременно с ним из B в A вышел второй путник. Они шли равномерно, но с разными скоростями.В момент встречи первому оставалось идти ещё16 часов, а второму — 9 часов. Через сколько часов после выхода они встретились?

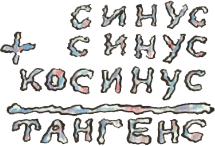2. Решите ребус

СИНУС + CИНУС + КОСИНУС = ТАНГЕНС.

Одинаковым буквам соответствуют одинаковые цифры, разным — разные.

3. Выпишем цифры от 0 до 9 подряд и рассмотрим последовательность сумм двух соседних цифр:

0		1		2		3		4		5		6		7		8		9
	1		3		5		7		9		11		13		15		17

В этой последовательности числа увеличиваются на 2. Расположите цифры от 0 до 9 таким образом, чтобы в образовавшейся последовательности сумм соседние числа увеличивались на 1.

4. Найдите все двузначные числа, равные сумме куба числа единиц и квадрата числа десятков.

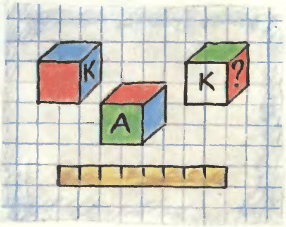5. Имеется три одинаковых детских кубика и линейка. Без вычислений измерьте большую диагональ кубика.

Задачи четвёртого номера 1990 года

1. Какой может быть последняя цифра квадрата целого числа, если предпоследняяцифра — нечётная?

2. В студенческом шахматном турнире приняли участие два школьника. Они вместе набрали 6,5 очков,а все студенты — поровну. Сколько студентов участвовало в турнире? (В турнире каждый участник играет с каждым по одному разу, за выигрыш дают1 очко, за ничью — 0,5 очка, за поражение — 0 очков.)

3. Решите ребус

КВАНТ + КВАНТ + КВАНТ = ЖУРНАЛ.

Одинаковым буквам соответствуют одинаковые цифры, разным — разные.

4. Докажите признак делимости на 13: число делится на 13 в том и только в том случае, если сумма учетверённой последней цифры и числа, полученного отбрасыванием последней цифры, делится на 13.

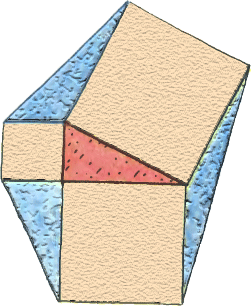5. На сторонах прямоугольного треугольника построены квадраты («пифагоровы штаны»). Их вершины соединены так, как показано на рисунке. Докажите равенство площадей образовавшихся треугольников.

Задачи пятого номера 1990 года

1. Антон пошёл в молочный магазин. Денег у него не было, но он взял пустые бутылки из-под молока — 6 литровых (по 20 копеек)и 6 пол-литровых (по 15 копеек). В магазинебыло только разливное молоко по цене22 копейки за литр. Антон решил сдать часть бутылок, а купленное на полученные деньги молоко налить в оставшиеся бутылки. Какое наибольшее количество молока он сможет принести домой? 

2. Самолёт вылетел из города A в полдень и приземлился в городе B в14 часов местного времени. В полночь он вылетел обратно и прилетел вгород A тогда, когда там было 6 часов утра. Сколько времени длится перелёт между этими городами на таком самолёте?

3. Решите ребус

EINS + EINS + EINS + EINS + EINS = FUNF.

Одинаковым буквам соответствуют одинаковые цифры, разным — разные.

4. Представьте число 1990 тремя различными способами в виде суммы нескольких (двух или больше) последовательных натуральных чисел.

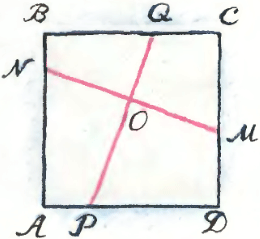5. В квадрате ABCD проведены два взаимно перпендикулярных отрезка MN и PQ. Покажите, что сумма периметров четырёхугольников APON иCQOM равна сумме периметров четырёхугольников BNOQ и DMOP.

Задачи шестого номера 1990 года

1. Незнайка хвастал своими выдающимися способностями умножать числа в уме. Чтобы его проверить, Знайка предложил ему написать какое-нибудь число, перемножить его цифры и сказать ему результат. 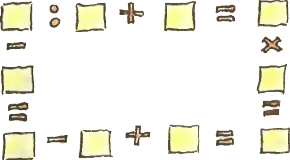«2310» — немедленно выпалил Незнайка, лишь успев записать число. «Не может быть»— ответил, подумав, Знайка. Как он обнаружил ошибку, не зная исходного числа?

2. Впишите в клеточки рисунка все числа от 1 до 10 так, чтобы выполнялись указанные на рисунке равенства. 

3. На шхуне капитана Врунгеля «Победа» (а потом «Беда») был четырёхзначный номер. Номер был примечателен тем, что являлся квадратом целого числа. Во время шторма смыло первую цифру, и номер стал кубом целого числа. После следующего шторма смыло следующую цифру, и номер стал четвёртой степенью целого числа. Какой номер был на шхуне?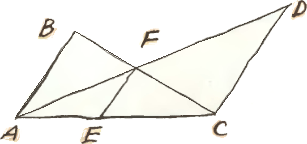

4. Отрезки АВ, EF и CD, изображённые на рисунке, параллельны. Докажите, что сумма отношений EF/AB и EF/CD равна 1.

5. На дискотеку собрался почти весь класс —22 человека. Рената танцевала с семью мальчиками, Ширинат — с восемью, Вера — с девятью и так далее до Ирины, которая танцевала со всеми мальчиками. Сколько мальчиков было на дискотеке?

Задачи седьмого номера 1990 года

1. Некий торговец каждый год увеличивал на одну треть свое состояние, уменьшенное на сто фунтов стерлингов, которые он ежегодно затрачивал на свою семью. Через три года торговец обнаружил, что его состояние удвоилось. Сколько денег было у торговца в начале? 

2. Решите ребус НЕ^П = ТУН. Одинаковым буквам соответствуют одинаковые цифры, разным —разные. 

3. Разрежьте изображённую на рисунке фигуру по линиям клеток на четыре конгруэнтные фигуры.

4. Какое четырёхзначное число обладает такими свойствами: оно само квадрат целого числа, а числа, образованные первыми двумя цифрами и последними двумя цифрами,— также полные квадраты?

5. Гулливер во время пребывания в Лапуте интересовался денежной системой этой страны. Ему рассказали, что в стране используют монеты в 1, 2 и4 лапти, сделанные из чистого золота. Монеты круглые, причём если положить монету в 1 лаптю на монету в2 лапти так, чтобы её край проходил через центр двухлаптевой монеты, то точки пересечения краёв монет лежат на диаметре однолаптевой монеты. То же соотношение размеров у монет в 2 и 4 лапти. Веса монет пропорциональны их номиналам. Толщина однолаптевой монеты — 1 мм. Какова толщина остальных монет?

Задачи восьмого номера 1990 года

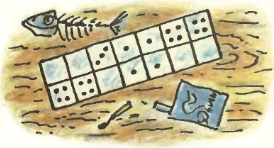1. В коробке лежит домино, как показано на рисунке. Как расположены кости в его верхнем ряду? 

2. Недавно сообщалось, что из-за понижения уровня Аральского моря его акватория (площадь) уменьшилась на 40%, а объём воды уменьшился на 60%.Может ли быть справедливым такое утверждение? А может ли получиться так, что уровень воды в водоёме упадёт и его акватория уменьшится на 60%, а объём воды уменьшится на 40%?

3. Решите арифметический ребус

ЛЕТО + ЛЕТО = ПОЛЕТ.

Одинаковым буквам соответствуют одинаковые цифры, разным — разные. 

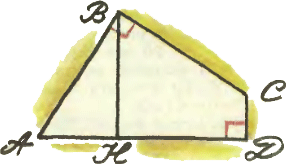4. Найдите площадь четырёхугольника ABCD, углы при вершинах B и D которого прямые, АВ = ВС, а длина высоты ВН равна 1.

5. Таблица розыгрыша предыдущего первенства мира по футболу в той подгруппе, где участвовала советская команда, выглядит так:

	В	Н	П	Мячи	Очки
СССР	2	1	0	9 – 1	5
Франция	2	1	0	5 – 1	5
Венгрия	1	0	2	2 – 9	2
Канада	0	0	3	0 – 5	0

С каким счётом сыграли команды между собой, если известно, что только два матча закончились одинаково?

Задачи девятого номера 1990 года

1. Цену на яблоки подняли на 20%. Продавцу для того, чтобы изменить ценник, оказалось достаточным поменять местами цифры стоимости килограмма яблок. Сколько стоили яблоки до их подорожания, если эта цена была меньше рубля?

2. Учитель задал на уроке замысловатую задачу. Количество мальчиков, решивших эту задачу, оказалось равным количеству девочек, её не решивших.Кого в классе больше — решивших задачу или девочек?

3. Решите арифметический ребус. Одинаковым буквам соответствуют одинаковые цифры,разным — разные. 

4. Два разных цилиндра имеют одинаковую боковую поверхность, равную 100 квадратным сантиметрам. Докажите, что можно вырезать из бумаги параллелограмм площадью 100 квадратных сантиметров, которым можно оклеить боковую поверхность как первого, так и второго цилиндра.

5. Школа находится на одной улице с моим домом. Однажды, идя в школу, я стал считать на моей стороне улицы сумму номеров домов, мимо которых я проходил. Когда сумма номеров сталаравна 99, перешёл через поперечную улицу. После этого я начал считать снова и насчитал сумму 117. Затем перешёл через ещё одну поперечную улицу. И в следующем квартале считал сумму номеров домов. Там она оказалась равной 235, включая и номер дома школы, которая стоит последней в этом квартале. В доме с каким номером живу я? Каков номер дома школы?

Задачи десятого номера 1990 года

1. Найдите все такие простые числа p, что числа p + 2 и p + 4 тоже простые.

2. В одной комнате находятся три выключателя, а в другой — три лампочки. Каждый выключатель обслуживает одну из лампочек. Как узнать, какой выключатель связан с какой лампочкой, если в комнату с лампочками можно войти лишь один раз?

3. Первое четырёхзначное число составлено из последовательных цифр, расположенных в порядке возрастания, второе число составлено из тех же цифр, но в порядке убывания, третье четырёхзначное число тоже составлено из этих четырёх цифр. Что это за числа, если их сумма равна 12 300?

4. Внутри квадрата расположен меньший квадрат, стороны которого соответственно параллельны сторонам большего квадрата. Вершины квадратов соединены так, как показано на рисунке. Докажите, что сумма площадей синих четырёхугольников равна сумме площадей красных четырёхугольников. 

5. Кооперативом была куплена партия товара и продана с прибылью в m рублей.На вырученные деньги была куплена другая партия того же товара и продана по прежним ценам; при этом прибыль составила m рублей. Сколько было уплачено за первую партию товара?

Задачи одиннадцатого номера 1990 года

1. Из двух одинаковых железных проволок кузнец сковал по одной цепи. Первая содержит 80 одинаковых звеньев, авторая — 100. Каждое звено первой цепи на5 граммов тяжелее каждого звена второй цепи. Какова была масса каждой проволоки?

2. Если Зa + 4b + 5c при некоторых целых значениях a, b и c делится на 11, то и9a + b + 4c при этих значениях a, b и cделится на 11. Докажите это. 

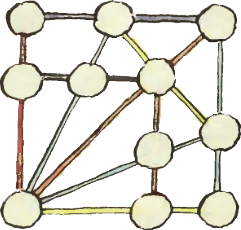3. Расставьте в кружках рисунка числа от 1 до 11 так, чтобы сумма трёх чисел на каждом из десяти отрезков была одна и та же. 

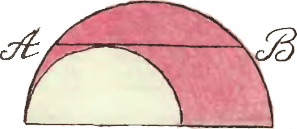4. Отрезок AB параллелен обоим диаметрам двух полукругов, расположенных, как показано на рисунке, касается меньшего полукруга и равен 24 см. Чему равна площадь фигуры, окрашенной в красный цвет? 

5. Два приятеля пришли на базар. Весёлый молодец продавал20 котов по цене от 12 до 15 рублей и 20 мешков по цене от30 копеек до 1 рубля. Цены всех котов и всех мешков разные. Докажите, что каждый из друзей может купить по коту в мешке так, чтобы они заплатили одинаковую сумму денег.

Задачи двенадцатого номера 1990 года

1. Несколько учеников отвечали на уроке, и все получили отметкине ниже тройки. Аня получила отметку, на 10 меньшую суммы отметок остальных; Боря получил отметку, на 8 меньшую суммы остальных отметок; Вера —отметку, на 6 меньшую суммы отметок остальных. Сколько человек отвечало на уроке и какие отметки они получили?

2. Замените в ребусе

А · Р = И – Ф = М : Е = Т – И = К : А

буквы цифрами так, чтобы выполнялись все равенства. (Одинаковым буквам соответствуют одинаковые цифры, разным — разные.)

3. Огромный военный оркестр демонстрировал своё искусство на площади. Сначала музыканты выстроились в квадрат, а затем перестроились в прямоугольник. Количество шеренг увеличилось на 5. Сколько музыкантов было в оркестре?

4. Может ли число, являющееся полным квадратом, записываться лишь с помощью цифр 0 и 6? 

5. Высота некоторой египетской пирамиды, выраженная в метрах, больше произведения двух нечётных двузначных чисел, но меньше квадрата их полусуммы. Для какого фараона она была построена?