«Квант» для «младших» школьников Задачи 1979 года

«Квант» для «младших» школьников

Задачи первого номера 1979 года

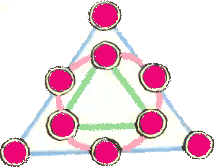1. Расставьте числа 1, 2, ..., 9 в красные кружочки рисунка так, чтобы сумма чисел по внутреннему треугольнику равнялась квадрату одного из этих чисел, сумма чисел поокружности — кубу того же числа, а сумма чисел по внешнему треугольнику — сумме квадрата и куба этого числа.

2. Был очень жаркий день, и четыре супружеские пары выпили 49 бутылок кока-колы. Анна выпила 2 бутылки,Бетти — 3, Сессиль — 4, Доротти — 5. Мистер Адаме выпил столько же, сколько и его жена, мистер Браун — вдвое,Вильсон — втрое, Грин — вчетверо больше своих жён. Назовите фамилию каждой из четырёх дам.

3. В одном племени приняты женские имена, составленные лишь из двух букв — А и В. Сочетания ААА и ВВ сами по себе что-то означают, но из состава более длинных слов их можно без ущерба вычёркивать (или вписывать). Сочетание ААВ в последнее время заменили на более культурное сочетание ВА, так что теперь они равнозначны. Можно ли верить вождю племени, который говорит, что у него шесть дочерей и всех их зовут по-разному?

4. Решите ребус АА^Н = АННА.

Задачи второго номера 1979 года

1.Несколько знатоков взялись за расшифровку числового ребуса

ТАМТАМ + МРАК = КОШМАР,

причём каждый из них получил верный ответ, отличный от ответов других. Знатоки исходили из того, что каждая буква означает некоторую цифру, причём разные цифры обозначены разными буквами. Сколько могло быть знатоков?

2. Сумма никаких двенадцати последовательных чисел натурального ряда не делится на 4. Докажите это.

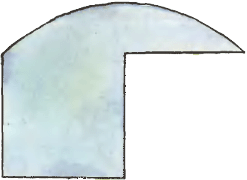3. Изображённую на рисунке фигуру разрежьте на две конгруэнтные части.

4. На столе стоят шесть стаканов. За один раз можно перевернуть любые пять из них. Можно ли, повторяя несколько раз эту операцию, поставить все шесть стаканов вверх дном? Обобщите эту задачу на случай чётного числа стаканов.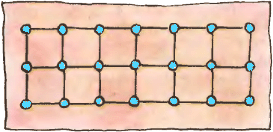 

5. В вершинах сетки, имеющей форму прямоугольника 2×10, помещена 3 · 7 = 21точка. Можно ли покрасить эти точки в два цвета так, чтобы ни одна четвёрка одноцветных точек не образовывала прямоугольник?

Задачи третьего номера 1979 года

1. Прочтите 14 зашифрованных цифрами слов: 5916, 1378, 609136, 6094, 9721, 591, 690958, 634, 7958, 8374, 61274, 790968, 4242025, 79691, заменив для этого в приведённом на рисунке примере на умножение буквы на цифры (одинаковым буквам соответствуют одинаковые цифры, одна и та же цифра может обозначаться разными буквами).

2. В языке некоторого племени любое сочетание восьми различных букв И, Г, Р, Ё, Т, Н, О, К является словом, и других слов нет. Вождь племени, узнав о существовании словарей, поручил своему придворному лингвисту составить аналогичный словарь из всех слов племени. Лингвист выписал буквы в порядке И, Г, Р, Ё, Т, Н, О, К и стал упорядочивать слова в соответствии с этим алфавитом. Он дошёл до слова ЁКОНТРГИ. Какое слово он должен написать следующим? А после слова ИЁНГТКОР? После слова ИГКОНТЁР? Какое слово будет последним?
3. В комнате стоят табуретки и стулья. У каждой табуретки 3 ноги, у каждого стула 4 ноги. Когда на всех табуретках и стульях сидят люди, в комнате всего 39 ног. Сколько стульев и сколько табуреток в комнате?
4. Два человека бегут по ступеням эскалатора метро. Первый бежит быстрее второго. Кто насчитает больше ступеней?

Задачи четвёртого номера 1979 года

1. В первом ребусе цифры зашифрованы фигурками, в остальных —буквами и звёздочками. Одинаковым фигуркам и буквам соответствуют одинаковые цифры, разным — разные; звёздочки могут быть любыми цифрами.Ни одно число не начинается нулём. Расшифруйте ребусы.
2. Решите в ненулевых цифрах уравнения
а) 1000x + 100y + 10z + z = (10x + y)²+ (10z + z)²;
б) 1000x + 100x + 10y + y = (10y + y)²+ (10x + x)².
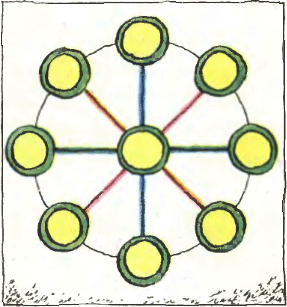3. В кружочки изображённого на рисунке числового колеса поставьте первые девять нечётных простых чисел так, чтобы сумма любых трёх чисел, расположенных по диаметру, была простым числом. Докажите, что при этом в центре может стоять любое из этих простых чисел, кроме числа 3.
4. Параллелограмм составлен из трёх равнобедренных треугольников, среди которых нет конгруэнтных. Найдите величины его углов.
5. Двое мальчиков играют в такую игру: они по очереди ставят ладьи на шахматную доску. Выигрывает тот, при ходе которого все клетки доски оказываются побитыми поставленными фигурами. Кто выигрывает в этой игре, если оба стараются играть наилучшим образом?

Задачи пятого номера 1979 года

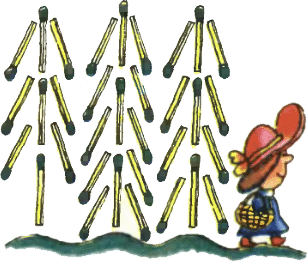1. На рисунке изображён лес (из спичек) и Красная Шапочка, идущая к бабушке. Переложите две спички так, чтобы Красная Шапочка возвращалась обратно. (Другими словами, переложите две спички от правого дерева к левому.)
2.Рассмотрим трёхзначное число. Найдём произведение его цифр. Затем найдём произведение цифр результата. Исходное число и два полученных произведения можно изобразить соответственно так, как показано на рисунке (одинаковые фигурки заменяют одинаковые цифры). Каким было исходное число? Сколько решений имеет задача?
3. Заполните свободные клетки шестиугольника натуральными числами так, чтобы в них оказались все числа от 1 до 19, и во всех пяти рядах каждого из трёх направлений (вертикального и двух наклонных) сумма чисел, стоящих в одном ряду, была бы одна и та же.
4. Студенты Вадим и Коля играют в шахматы. Мимо проходит Надя — младшая сестра Коли. На вопрос, сколько лет Наде, Коля ответил так: «Если умножить номер сегодняшнего дня недели на число дня рождения Нади и на номер месяца, в котором она родилась, то получится год рождения Нади». В какой день недели Вадим и Коля играли в шахматы?
5. Профессор Тестер проводит серию тестов, на основании которых он выставляет испытуемому средний балл. Ответив на последний тест, Джон понял, что если бы за этот последний тест он получил 97 очков, то его средний балл равнялся бы 90. С другой стороны, если бы он получил за последний тест всего 73 очка, то его средний балл составил бы 87. Сколько тестов в серии профессора Тестера?

Задачи шестого номера 1979 года

1. Длина одной стороны треугольника равна 6,31 м, длина другой стороны — 0,82 м. Чему равна длина третьей стороны, если она выражается целым числом метров?

Ответ   Указание   Решение

2. На окружности расположены одна красная точка и 1977 белых. Рассматриваем всевозможные многоугольники с вершинами в этих точках. Каких среди них будет больше: с красной вершиной или без неё?
3. Пусть a — произвольное 1979-значное число, делящееся на 9. Сумму цифр этого числа обозначим буквой A.Сумму цифр числа A обозначим буквой B. Сумму цифр числа B — буквой C. Найдите число C.
4. На клетке h8 шахматной доски мелом написано +1, а во всех остальных клетках —число –1. За одну операцию разрешено сменить все знаки на противоположные либо на одной (любой) вертикали, либо на одной (любой) горизонтали. Докажите, что сколько бы операций мы ни выполнили, мы никогда не получим +1 во всех клетках доски одновременно.
5. Три курицы за три дня снесли три яйца. Сколько яиц снесут двенадцать кур за двенадцать дней?

Задачи седьмого номера 1979 года

1. Заполните пустые клетки таблицы так, чтобы сумма чисел, стоящих в любых трёх подряд идущих клетках, равнялась пятнадцати.

6

4

2. Из спичек римскими цифрами составлено неверное равенствоIVI – III = IX. Переложите одну спичку так, чтобы получилось верное равенство.
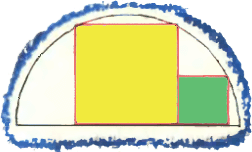3. Два квадрата расположены внутри полукруга так, как показано на рисунке. Докажите, что площадь большего квадрата в четыре раза превосходит площадь меньшего квадрата.
4. Девять одинаковых книг стоят меньше десяти рублей, а десять таких же книг стоят больше одиннадцати рублей. Сколько стоит одна книга?
5. Майя использовали очень интересный способ записи чисел: на рисунке показано, как майя записывали числа 1, 5, 17, 137. Поймите, почему эту систему счисления считают двадцатеричной, и запишите в ней число 1979.

Задачи восьмого номера 1979 года

1. Разность двух квадратов натуральных чисел оканчиваетсяцифрой 2. На какие цифры оканчиваются уменьшаемое и вычитаемое, если последняя цифра уменьшаемого больше последней цифры вычитаемого?
2. Найдите все двузначные числа, каждое их которых является делителем трёхзначного числа, полученного вписыванием нуля между первой и последней цифрами самого двузначного числа.
3. В футбольном турнире каждая пара команд должна встретиться между собой один раз. В среду, после очередного тура, Боря подсчитал, что чётное число встреч провели семь команд. После следующего тура Боря обнаружил, что чётное число встреч по-прежнему имеют семь команд! Возможно ли такое? Если да, то можно ли определить, сколько команд участвовало в турнире? (Расписание турнира составлено так, что в каждом туре свободна не более чем одна команда.)
4. Коля отправился за грибами где-то между восемью и девятью часами утра, в момент, когда стрелки его часов были совмещены. Домой он вернулся между двумя и тремя часами дня; при этом стрелки его часов были направлены в прямо противоположные стороны. Сколько длилась прогулка Коли?
5. Сколькими способами девять конгруэнтныхквадратиков — три красных, три белых и три синих,— можно расположить в виде квадрата 3×3 так, чтобы в каждой строке и в каждом столбце встречались квадратики всех цветов?

Задачи девятого номера 1979 года

1. Если Аня идёт в школу пешком, а обратно едет на автобусе, то всего на дорогу она затрачивает полтора часа. Если же она едет на автобусе в оба конца, то весь путь занимает у неё тридцать минут. Сколько времени тратит Аня на дорогу, если и в школу, и из школы она идёт пешком?
2. Может ли сумма первых нескольких натуральных чисел оканчиваться на 1979?
3. На колхозный двор прилетело 35 ворон. Неожиданно испугавшись чего-то, вороны взлетели и разделились на две стаи: первая стая уселась на ветви старого тополя, а другая — на крышу водонапорной башни. Через некоторое время с тополя на крышу перелетело 5 ворон, столько же ворон совсем улетело с крыши, после чего на тополе осталось вдвое больше ворон, чем на крыше. Сколько было ворон в обеих стаях первоначально?
4. Найдите произведение разностей, полученных вычитанием из числа 1дробей, числители которых равны 1, а знаменатели равны квадратам чисел 2, 3, ..., 14, 15.

5. Возьмите трёхзначное число. Запишите цифры в обратном порядке, получится ещё одно трёхзначное число. От большего числа отнимите меньшее: например, 743 – 347 = 396. Последнюю цифру разности сообщите отгадчику. Отгадчик сможет назвать разность. Как он это сделает?

Задачи десятого номера 1979 года

1.Туристы купили в магазине сто предметов: спички (цена — 1 копейка за коробку), пирожки (по 10 копеек) и консервы (цена — 50 копеек за банку). За все уплатили 5 рублей. Сколько предметов каждого товара куплено?
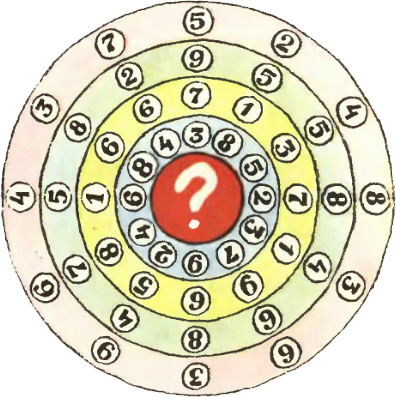2. Поверните изображённые на рисунке четыре кольца так, чтобы сумма любых четырёх чисел, расположенных на одном paдиусе, равнялась одному и тому же числу. Какое это число?
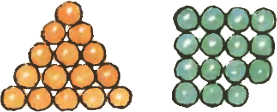3. 15 шариков можно сложить в виде треугольника, но нельзя сложить в виде квадрата — одного шарикане хватает. Из какого количества шариков, не превосходящего 50, можно сложить как треугольник, так и квадрат?
4. Можно ли в квадрат со стороной 1 поместить несколько непересекающихся кругов, сумма радиусов которых равна 1979?
5. В ряд расположено пять монет. Средняя лежит вверх орлом,остальные — решкой. За один ход разрешено перевернуть любые три рядом лежащие монеты. Можно ли добиться, чтобы все монеты лежали вверх орлом? А если вверх орлом первоначально лежит только первая монета? А если только вторая?

адачи одиннадцатого номера 1979 года

1. Разрежьте бумажный прямоугольник 1,5×4 на две части так, чтобы ими можно было оклеить куб с ребром 1.
2. Сумма всех натуральных чисел от 1 до любого числа, оканчивающегося на 5, сама делится на 5. Докажите это.
3. Восемьдесят спичек были разложены на пять кучек. Из первой кучки взяли пятую часть бывших в ней спичек и переложили во вторую кучку. Затем из второй кучки пятую часть оказавшихся в ней после перекладывания спичек переложили в третью кучку, и так далее. Наконец, из пятой кучки переложили пятую часть оказавшихся в ней спичек в первую кучку. Во всех кучках спичек стало поровну. Сколько спичек было в кучках до перекладывания?
4. Существует ли треугольник, длины высот которого равны 1, 2 и 3 соответственно?
5. Турист хочет приготовить себе на завтрак два яйца всмятку и ещё четыре сварить вкрутую, чтобы взять их в дорогу. Яйца всмятку варятся 2 минуты, авкрутую — 4 минуты(яйца кладут в кипящую воду). За какое наименьшее время турист может сварить яйца, если у него есть кастрюлька вместимостью четыре яйца?

Задачи двенадцатого номера 1979 года

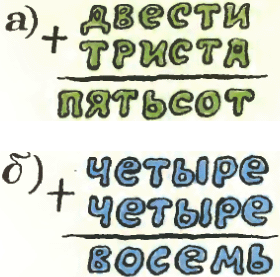1. а) В ребусе ДВЕСТИ + ТРИСТА = ПЯТЬСОТ использованы все десять цифр.Буква О обозначает цифру 0, буква П — ту же цифру, что И, а буква В — ту же,что Я, остальные буквы имеют самостоятельные цифровые значения. Расшифруйте ребус!
б)В ребусе ЧЕТЫРЕ + ЧЕТЫРЕ = ВОСЕМЬ тоже использованы все десять цифр. Нет букв, имеющих одинаковые значения, зато известно, что Ч^Е = С, причём Е —нечётная цифра. Расшифруйте и этот ребус тоже!
2. Мальчик купил на рубль почтовых марок, причём двухкопеечных марок он купил в 10 раз меньше, чем однокопеечных, остальные же марки были пятикопеечными. Сколько марок каждого достоинства купил мальчик?
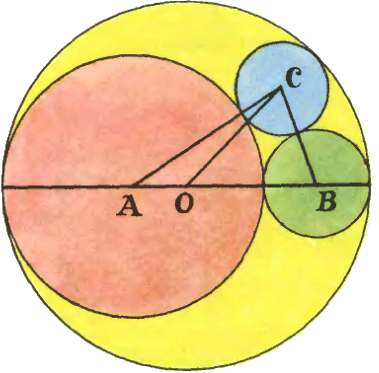3. На диаметре окружности с центром в точке O находятся центры A и B ещё двух окружностей, касающихся как первоначальной окружности, так и одна другую. Окружность с центром Cкасается всех трёх рассмотренных ранее окружностей, как на рисунке. Докажите, что периметры треугольников AOC и BOCравны длине диаметра первой окружности.

4. Ученик 6 класса Петя Иванов придумал две новые теоремы:
а) если натуральное число делится на 27, то и сумма его цифр делится на 27;
б) если сумма цифр натурального числа делится на 27, то и само число делится на 27.
Сможет ли Петя доказать эти теоремы?