«Квант» для «младших» школьников Задачи 1996 года

«Квант» для «младших» школьников

Задачи первого номера 1996 года

1. У крестьянина были коза, корова и кобыла, а ещё стог сена. Сын крестьянина подсчитал, что этого сена хватит, чтобы кормить козу и кобылу1 месяц, или козу и корову ³/₄ месяца, или же корову и кобылу ¹/₃ месяца.В ответ на это отец заметил, что сын плохо учится в школе. Прав ли он?

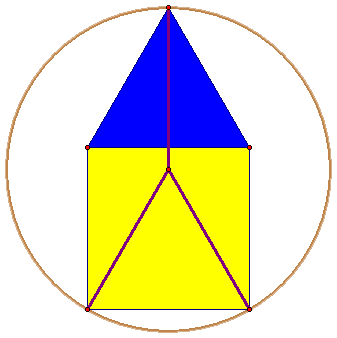2. На стороне AB квадрата ABCD вне него построен равносторонний треугольник ABE. Чему равен радиус окружности, проходящей через точки C,D и E, если длина стороны квадрата равна a?

3. Разъезжаясь на зимние каникулы, 19 друзей-студентов дали обещание писать друг другу письма. Каждый отправил из дома друзьям 2 или 4 письма. Могло ли случиться, что каждый из них получил ровно по три письма?

4. Разместите на плоскости шесть точек, чтобы каждые пять из них можно было покрыть двумя квадратами с диагоналями длины 1, но все шесть нельзя было покрыть двумя кругами с диаметрами 1.

5. 100 чиновников министерства были приглашены на совещание. Кресла были расставлены в виде прямоугольника в 10 рядов по 10 кресел. Начало совещания задерживалось, и разместившиеся в креслах чиновники стали обмениваться со своими соседями сведениями о зарплатах. Те чиновники, которые убедились, что из всех их соседей слева, справа, спереди, сзади и по диагоналям не более чем один человек получает больше, стали считать себя высокооплачиваемыми. Какое наибольшее число чиновников могли считать себя высокооплачиваемыми?

Задачи второго номера 1996 года

1. Продолжите последовательность 2, 9, 10, 12, 19, 20, 21, ...

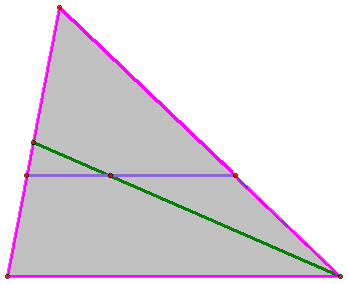2. В треугольнике ABC проведены медиана ВМ и отрезок РК, параллельный стороне АВ. Отрезки ВМ и РК пересекаются в точке X, которая делит отрезокРК на части РХ длиной 2 и ХК длиной 3. Найдите длину стороны AB.

3. Из произведения

1! · 2! · 3! · ... · 99! · 100! можно вычеркнуть один из ста сомножителей так, чтобы произведение стало точным квадратом. Докажите это. (Запись n! означает произведение всех натуральных чисел от 1 до n.)

4. Можно ли какими-нибудь тремя треугольниками оклеить куб в один слой? А четырьмя?

5. Назовём коневым расстоянием между двумя полями шахматной доски наименьшее количество ходов коня, необходимое, чтобы попасть с одного из этих полей на другое, а королевскимрасстоянием — наименьшее количество ходов короля для перехода с одного поля на другое.
Среди пар полей шахматной доски, коневое расстояние между которыми равно 4, найдите те, королевское расстояние между которыми наименьшее. Чему равно это расстояние?

Задачи третьего номера 1996 года

1. В двух кошельках лежит 20 тысяч рублей, причём в одном из них денег вдвое больше, чем в другом. Может ли такое быть?

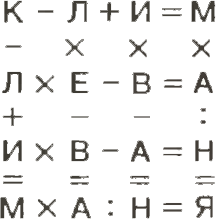2. Замените буквы цифрами так, чтобы все равенства рисунка оказались верными.Одинаковым буквам соответствуют одинаковые цифры, разным — разные.

3. В нижеследующем тексте восстановите пропущенные числа, обращая внимание на грамматическую правильность получаемого текста.

«Алиса на ... года старше Орлёнка Эдда и на ... года старше Ореховой Сони. Пичужке сегодня исполнился ... год. Ореховой Соне в позапрошлом году было... года, а сейчас она на ... года моложе Орлёнка Эдда. Сколько лет каждому из них, если сумма их возрастов составляет ... года, через год сумма возрастов Алисы и Пичужки составит ... лет, а ни одному персонажу не исполнилось ещё десяти лет?»

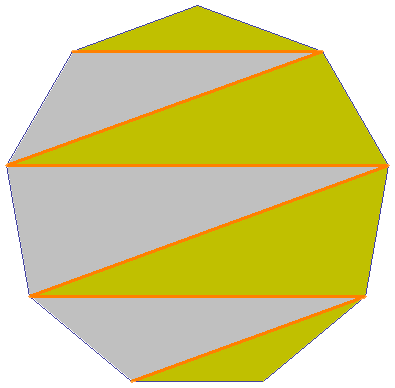4. Зигзаг диагоналей разделил правильный девятиугольник на треугольники, как показано на рисунке. Окрашенная каким цветом часть площади больше?

5. Можно ли выбрать из каждого слова фразы, которую вы сейчас читаете, по одной букве так, чтобы все эти буквы были различными буквами русского алфавита (заглавные и прописные буквыне различаем)?

Задачи четвёртого номера 1996 года

1. Существуют ли два таких простых числа, сумма и разность которых вновь простые числа?

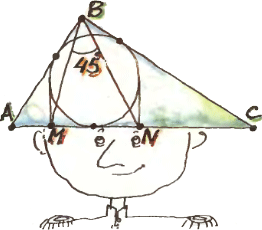2. В прямоугольный треугольник ABCвписали окружность. Её проекция на гипотенузу AC — отрезок MN. Докажите, что величина угла MBN равна 45°.

3. Алёша вышел из поселка Алёшино в 10 часов 18 минут и двигался с постоянной скоростью. В тот же день Борис вышёл из Борисова в 9 часов.Дорога пересекает широкую реку. Алёша и Борис одновременно подошли к мосту через эту реку, каждый со своей стороны. Алеша ушёл с моста на одну минуту позже Бориса и пришёл в поселок Борисово в половину второго — успел к обеду. Борис пришёл в Алёшино даже раньше: без 20 минут двенадцать. Когда они подошли к мосту?

4. Значение выражения 1995² + 1995² · 1996² + 1996² является квадратом целого числа. Докажите это.

5. Стекольщику заказали 85 квадратных пластинок 10×10 см из особого стекла. Он принял заказ, зная, что у него есть такое стекло размером 1×1 м, и поэтому надеясь суметь вырезать даже 100 таких пластинок. Но, замерив заново в мастерской своё стекло, стекольщик обнаружил, что оно имеет размер 99×99 см. Сможет ли он исполнить заказ?

Задачи пятого номера 1996 года

1. Азбукой Морзе записано слово: ·———————. Однако не сделаны пробелы между буквами. Прочитайте это слово. Напомним значения некоторых букв:

А	В	Е	М	О	Т
·—	·——	·	——	———	—

2. Буратино и Папа Карло планировали положить свои капиталы на общий счёт в банк «Навроде» под 500% годовых, рассчитывая через год забрать вклад величиной 900 золотых. Крах банка изменил их планы. Папа Карло положил свои деньги в банк «Вампириал» под 50% годовых, а Буратино — в банк «Обирон», даже не поинтересовавшисьпроцентной ставкой. Ровно через год они забрали свои вклады. Папа Карло получил 150 золотых, а Буратино в три раза меньше. Какой процент годовых даёт банк «Обирон»?

3. Три предпринимателя приехали в воинскую часть, в которой они когда-то служили, и привезли с собой подарки. Когда все 252 солдата были построены в одну шеренгу, первый предприниматель вручил подарки каждому четвёртому солдату, второй — каждому седьмому, а третий — каждому девятому солдату. Сколько солдат получили подарки, а сколько не получили?

4. Вася подписался на целый год на журнал «Квант». Однако почта работала плоховато, и он получил не все, что полагались, а только лишь большую часть причитающихся номеров журнала и меньшую часть причитающихся приложений. Оказалось, что сумма номеров полученных журналов в 5 раз превосходит количество полученных приложений. Без каких номеров журнала остался Вася?

5. Может ли квадрат целого числа оканчиваться цифрами 1996?

Задачи шестого номера 1996 года

1. Путешественник попал на остров, где живут правдивые — говорящие только правду, и лжецы — говорящие только ложь. Зайдя как-то раз в один дом, он встретил там несколько жителей. Путешественник спросил одного из них: «Сколько здесь лжецов?» И получил ответ: «По крайней мере один из нас — лжец.» Кем был отвечавший?

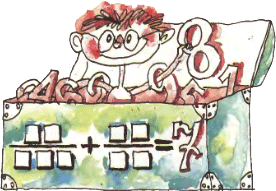2. Расставьте числа от 1 до 9 в клетки рисунка так, чтобы равенство оказалось верным.

3. Вова обнаружил, что в 1996 году возраст его мамы равен произведению цифр её года рождения. И с удивлением заметил, что то же самое верно и для его бабушки. Определите их возрасты.

4. Для любых целых чисел a, b и c число

(a – b)³(c – b) + (b – c)³(a – c) + (c – a)³(b – a)

является квадратом целого числа. Докажите это.

5. Замените буквы цифрами так, чтобы равенство

МЛРД · МИН = 1901 · ГОД

оказалось верным. (И на самом деле миллиард минут — это 1901 год!) Одинаковым буквам соответствуют одинаковые цифры, разным — разные.