«Квант» для «младших» школьников Задачи 2005 года

«Квант» для «младших» школьников

Задачи первого номера 2005 года

1. У продавца есть 3 сорта зелёного чая. Петя купил по несколько граммов каждого сорта. Продавец заметил, что если бы он поменял местами любые два ценника, а Петя купил такой же товар, то Пете пришлось бы заплатить больше денег. Могло ли такое случиться?

2. а) Можно ли, используя каждую из 10 цифр по одному разу, записать натуральное число и его квадрат?
б) А можно ли при тех же условиях записать квадрат и куб одного и того же натурального числа?

3. Петя: Успешно ли ты выступил на соревнованиях?
Вася: А ты реши сам. Меня обошла одна n-я часть спортсменов, зато я оставил позади одну (n – 1)-ю часть.
Петя: А что такое n?
Вася: Это некоторое натуральное число, большее 2.
Петя: О, поздравляю! Тебе удалось занять призовое третье место!
Не ошибся ли Петя?

4. Бильярдный стол имеет форму прямоугольного треугольника. Из точки на гипотенузе перпендикулярно ей выпустили шар, который ударился о два борта и вернулся на гипотенузу. Докажите, что длина такого пути не зависитот точки старта. (Шар отражается от бортов по закону «угол падения равен углу отражения».)

5. Многим известна компьютерная игра «Сапёр». Предположим, в некоторых клетках квадрата 9×9 стоят невидимые мины. Кроме того, в каждой клетке (даже в той, где есть мина) записано общее количество мин в соседних с ней клетках. Соседними называем клетки, имеющие общую сторону или вершину. Можно ли по этим числам определить расположение всех мин?

Задачи второго номера 2005 года

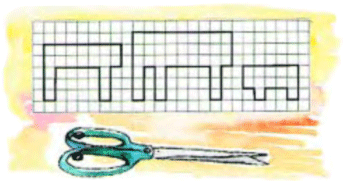1. Разрежьте каждую из трёх фигур, изображённых на рисунке, на две конгруэнтные части.

Ответ

2. Если звонить с обычного телефона на сотовый, то оплату разговора производит владелец сотового телефона. Если же звонить с обычного телефона на обычный, либо с сотового на любой, то за разговор платит тот, кто звонил. Восемь бизнесменов в течение дня перезванивались между собой и сделали по три звонка каждый. При этом все владельцы сотовых телефонов уплатили за разное число разговоров. У Иванова, Петрова, Сидорова и Кузнецова — сотовые телефоны, у Адамова иДавыдова — обычные. Какой телефон у Джапаридзе?

3. Можно ли в клетки таблицы размера 4×4 вписать числа от 1 до 16 (каждое по одному разу) так, чтобы произведения всех чисел в каждом квадрате 3×3 были равны?

Ответ   Решение

4. Профессор Мумбум-Плюмбум ищет 6 натуральных чисел, среди которых ровно одно число делится на 6, ровно два числа делятся на 5, ровно три числа делятся на на 4, ровно четыре числа делятся на 3, ровно пять чисел делятся на 2,ровно шесть чисел делятся на 1. Существуют ли они?

Ответ   Решение

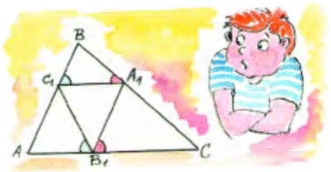5. В треугольник ABC вписан равносторонний треугольник A₁B₁C₁ так, что величина угла BC₁A₁ равна величине угла C₁B₁A, а величина угла BA₁C₁ равна величине угла A₁B₁C. Докажите, что треугольник ABC равносторонний.

Задачи третьего номера 2005 года

1. Из репортажа корреспондента журнала «True-False»: «Я вместе с рыцарями и лжецами лечу на борту воздушного лайнера. Вы, конечно, знаете, что рыцари всегда говорят правду, а лжецы всегда безбожно лгут... На мой вопрос «Сколько же здесь лжецов?» каждый из моих попутчиков отвечал: «Лжецов в салоне нечётное количество». После чего махал мне ручкой и выпрыгивал с парашютом. И вот я остался один...» Можно ли доверять корреспонденту журнала «True-False»?

Ответ   Указание

2. Когда Торопыжка хочет записать какую-нибудь дату, он пишет число и номер месяца (именно в таком порядке) арабскими цифрами, не оставляя между ними пробела,не помещая никакого разделительного знака и не ставя нулей в начале числа. Сколько дат в году нельзя различить при такой форме записи?

Ответ   Решение

3. На Поле Чудес мышиные норки расположены на различных расстояниях друг от друга, причём от каждой норки к ближайшей к ней по прямой линии протоптана тропинка. Какое наибольшее число тропинок может подходить к какой-либо норке?

4. Чичиков покупал у Плюшкина беглые души. Если бы он купил столько душ, сколько копеек заплатил за каждую, то Плюшкину досталось бы больше десяти рублей. А если бы он за каждую душу заплатил столько копеек, сколько купил душ, то Плюшкин получил бы больше шестидесяти рублей. Сколько душ и по какой цене купил Чичиков, если он израсходовал на это не более 25 рублей?

5. 50 синих и 50 красных точек разделили окружность на 100 равных дуг. Докажите, что прямоугольных треугольников, все вершины которых красные, существует столько же, сколько прямоугольных треугольников, все вершины которых синие.

Указание I   Указание II

Задачи четвёртого номера 2005 года

1. Профессор Мумбум-Плюмбум пытается найти треугольник, медиана которого делит его на два подобных между собой, но не конгруэнтных треугольника. Удастся ли ему это сделать?

2. Я забыл домашний номер телефона моего приятеля, но точно помню, что в его семизначном номере все цифры различны, квадраты трёх из них равны произведению двух соседних с ними цифр, а само семизначное число без остатка делится на 36.Какой номер телефона у моего приятеля?

3. Среди 2n + 1 последовательных натуральных чисел сумма первых n + 1 чисел равна сумме остальных. Докажите, что наименьшее из этих чисел является полным квадратом.

4. На двух чашках весов лежат гирьки так, что весы показывают равновесие. Все эти гирьки разложили по чашкам иначе, но так, что весы вновь показали равновесие. В третий раз на левую чашку поместили только те гирьки, которые оба раза уже были на ней. И на правой чашке оставили только те гирьки, которые оба раза уже были на ней. Будет ли вновь на весах равновесие?

5. Пете дали квадрат 8×8, в котором изначально были закрашены 7 клеток, и разрешили закрашивать другие клетки, руководствуясь следующим правилом. Если незакрашенная клетка граничит сторонами (не вершинами) с двумя закрашенными ранее клетками, то её также можно закрасить. Может ли случиться, что Петя закрасит весь квадрат?

Задачи пятого номера 2005 года

1. В одном магазине продавались английские буквы для номеров домов. Одинаковые буквы стоят одинаково, а разные имеют различные цены. Слово ONE стоит 6 долларов,слово TWO стоит 9 долларов, а слово ELEVEN стоит 16 долларов. Сколько стоит слово TWELVE?

2. В кубической коробке лежат несколько шаров. Наk-й грани коробки, где k = 1, 2, ..., 6, написано следующее утверждение: «В этой коробке больше 10 + k шаров». Лишь три утверждения верны. Сколько шаров в коробке?

3. Могут ли высота, медиана и биссектриса, проведённые из разных вершин треугольника, пересекаясь внутри этого треугольника, образовать правильный треугольник?

4. Можно ли, используя по одному разу каждую из цифр от 1 до 9, составить число, обладающее следующими свойствами:

• если вычеркнуть двойку, то оно поделится на 2;
• если вычеркнуть тройку, то оно поделится на 3;
• если вычеркнуть четвёрку, то оно поделится на 4;
• если вычеркнуть пятёрку, то оно поделится на 5;
• если вычеркнуть шестёрку, то оно поделится на 6;
• если вычеркнуть семёрку, то оно поделится на 7;
• если вычеркнуть восьмёрку, то оно поделится на 8;
• если вычеркнуть девятку, оно поделится на 9?

Можно ли сделать то же самое, используя каждую из цифр от 0 до 9?

5. Скучая в отсутствие покупателей, продавец расположил набор из ста гирек массами 1, 2, 3, ..., 100 граммов в произвольном порядке: m₁, m₂, ..., m₁₀₀. Покупатель заявил, что гирьки массами |m₁ – 1|, |m₂ – 2|, ..., |m₁₀₀ – 100| можно расположить на двух чашах весов так, что они окажутся в равновесии. Он сумел это доказать, не прибегая к взвешиваниям. Докажите и вы.

Задачи шестого номера 2005 года

1. Я собрал коллекцию старых календарей за последние 30 лет. Какими из них можно пользоваться в 2006 году? (Числа месяца и дни недели в используемом календаре должны соответствовать числам месяца и дням недели в календаре 2006 года.)

2. В классе на доске кто-то мелом написал: «С НОВЫМ ГОДОМ!» Дед Мороз и Снегурочка играют, стирая по очереди буквы (начинает Снегурочка). Каждый может своим ходом стереть либо одну любую букву, либо сразу несколько одинаковых букв. Выигрывает тот, кто сотрет последнюю букву и оставит на доске только восклицательный знак. Кто из игроков может обеспечить себе победу при любой игре партнёра?

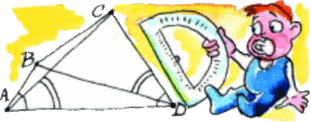3. Величины углов BAD и BAD равны 60°, величины углов CAD и CDB равны. Докажите равенство AB + CD = AD.

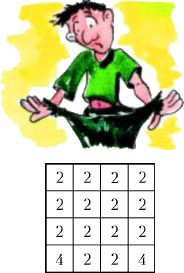4. Человек Рассеянный с улицы Бассейной перемещается по клеткам квадрата 4×4. Находясь в клетке, он теряет в ней 1 рубль, после чего переходит в соседнюю по стороне клетку. Там он снова теряет 1 рубль,после чего переходит в соседнюю клетку и так далее. Уборщица сообщила, сколько рублей она нашла в каждой клетке. Мог ли Человек Рассеянный с улицы Бассейной передвигаться так, чтобы рисунок соответствовал его перемещениям?

5. Среди 8 подозреваемых имеется один фальшивомонетчик. Будучи опрошены по отдельности, все отрицают причастность к преступному промыслу. Все осведомлены о роде занятий друг друга, но стесняются называть имя преступника. Инспектор Варнике может выделить любую группу из этих 8 человек и задать вопрос: «Есть ли среди вас фальшивомонетчик?» Если в группе нет фальшивомонетчика, то все отвечают «нет», в противном случае отвечают «да» («да» отвечает и сам фальшивомонетчик, пытаясь слиться с окружающими и не выдать себя). За какое наименьшее количество вопросов инспектор может гарантированно определить преступника?