«Квант» для «младших» школьников Задачи 2002 года

«Квант» для «младших» школьников

Задачи первого номера 2002 года

1. На кубик из воска сели отдохнуть несколько пчёл (их можно считать точками). На всех гранях количества пчёл разные. Какое наименьшее число пчёл могло отдыхать на кубике?

2. Придумайте два различных десятизначных числа, каждое из которых является кубом, причём одно из них получается из другого перестановкой цифр в обратном порядке.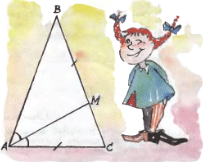

3. В треугольнике ABC, в котором AB = ВС, проведена биссектриса AM. Найдите величины углов треугольника, если ВМ = АС.

4. Можно ли число 2¹⁰⁰ представить в виде суммы квадратов трёх натуральных чисел?

5. В середине одной из стен квадратной комнаты 3×3 имеется проход шириной 1. Можно ли в эту комнату внести какой-нибудь стол, площадь которого больше 4?

Задачи второго номера 2002 года

1. — Задумай двузначное число,— предложил учитель Пете.— Задумал?
— Да.
— А теперь сумму его цифр умножь на 11 и от результата отними задуманное число. Сколько у тебя получилось?
— Двадцать пять.
— Тогда ты задумал... Какое число задумал Петя?

2. В кружке кройки и шитья седьмая часть всех участников — мальчики. После того как в кружок записались ещё 13 человек, количество мальчиков увеличилось, а их доля уменьшилась. На сколько увеличилось количество девочек в кружке?

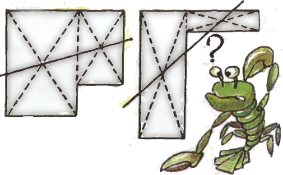3. На рисунке показаны два шестиугольника, каждый из которых Рак своими клешнями пытается разделить прямой линией на две части одинаковой площади. Ему удалось разделить первый шестиугольник, проведя прямую линию через центры двух прямоугольников, однако второй шестиугольник этим способом делится нена 2, а на 3 части. Тем не менее, его можно разделить и на 2 части. Помогите Раку это сделать.

4. 20 гирек равномерно расставлены по кругу. Всякие две противоположные гирьки отличаются по массе на 1 г. Докажите, что существуют 10 подряд стоящих гирек, общая масса которых равна общей массе остальных десяти.

5. Можно ли из последовательности натуральных чисел 10, 11, 12, ... выбрать несколько так, чтобы их произведение равнялось произведению нескольких первых чисел натурального ряда?

Задачи третьего номера 2002 года

1. Брат и сестра имеют одну фамилию, но я не смог назвать фамилию брата, узнав фамилию сестры. Как такое могло случиться?

2. Чтобы почтовый индекс журнала «Квант» легче запомнился, решите ребус

ИНДЕКС – КВАНТА = 117 296.

Одинаковые буквы означают одинаковые цифры, разные буквы — разные цифры.

3. Не имея никаких иных инструментов, кроме ножниц, разрежьте два бумажных квадрата площадью 9 и 16 квадратных единиц на прямоугольные куски, из которых можно составить квадратный лист площадью 25 квадратных единиц?

4. Можно ли представить число 100 в виде суммы ста последовательных целых чисел? А число 101 — в виде суммы ста одного последовательного целого числа?

5. Штирлиц должен передать в Центр набор из четырёх секретных натуральных чисел {а, b, c, d}. Чтобы никто не догадался, он отправил набор чисел{а + b, а + c, а + d, b + c, b + d} неизвестно в каком порядке. Центр, получив от Штирлица числа 13, 15, 16, 20, 22, расшифровал сообщение и нашёл набор из четырёх секретных чисел. Какие числа Штирлиц должен был передать в Центр?

Задачи четвёртого номера 2002 года

1. Мама и папа записали по одному натуральному числу, меньшему 100, не показав их друг другу. Папа утверждает, что сумма цифр произведения записанных ими чисел равна 18.Какое число задумал папа?

2. Всякая из десяти палочек имеет длину 19 сантиметров. Каждую из них разломили на две — получили двадцать палочек. Среди нихне нашлось двух палочек, разница длин которых больше9 сантиметров. Найдутся ли среди них две палочки, разница длин которых меньше полсантиметра? 

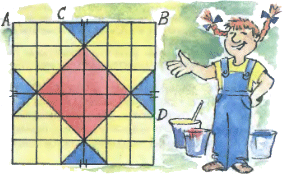3. В показанной на рисунке симметричной фигуре красная площадь равна синей. Чему равна длина стороны квадрата АВ, если длина отрезка CD — 3 сантиметра?

4. Сумма некоторых десяти целых чисел равна нулю. Докажите, что сумма пятых степеней этих чисел делится на 5.

5. Найдите наименьшее число, которое можно представить в виде суммы семи последовательных натуральных чисел, суммы одиннадцати последовательных натуральных чисел или суммы тринадцати последовательных натуральных чисел, но нельзя представить в виде суммы двух последовательных натуральных чисел.

Задачи пятого номера 2002 года

1. Один математик сказал: «Я родился в двадцатом столетии до начала Великой Отечественной войны. Год моегорождения — простое число, все цифры которого отличны от нуля. Произведение же цифр этого числа — точный квадрат». В каком году родился математик?

2. Дана точка A и прямая, не проходящая через точку A. На прямой отметили четыре точки и соединили каждую с точкой A. Могут ли все 6 треугольников,которые возникли на таком чертеже, быть равнобедренными?

3. Дети гуляют во дворе детского сада. Тех из них, у кого на ногах надето поровну носков, в 5 раз меньше, чем тех, у кого не поровну (каждый ребенок мог надеть как свои собственные носки, так и произвольное количество носков своих соседей). Воспитательница велела детям переодеться, и каждый ребенок снял с одной своей ноги носок и надел его на другую ногу. Теперь тех, у кого носков на ногах поровну, стало в 2 раза меньше, чем тех, у когоне поровну. Могло ли быть так, что в начале прогулки более чем у половины детей на одной ноге было ровно на один носок меньше, чем на другой?

4. Может ли число, десятичая запись которого выглядит как ххуу, где х и y — некоторые цифры, быть полным квадратом? А число, запись которого имеет вид xxxyyy?

5. Если величины всех углов выпуклого двенадцатиугольника кратны 30°, то величины всех его углов равны. Докажите это.

Задачи шестого номера 2002 года

1. Число УГУ делится на 13. Обязательно ли делится на 13 число ГУГ? (Числа записаны в десятичной системе счисления; одинаковыми буквами обозначены одинаковые цифры, разными буквами —разные цифры.)

2. Генный инженер Пупкин может из одной особи создать другую, у которой количество носов на 1 меньше количества ушей или количество ушей в 2 раза больше количества носов, чем у первой особи. Какое самое меньшее количество ушей должно иметь одноносое существо, чтобы из него генный инженер Пупкин, многократно применяя свой способ, смог вывести существо с 33 носами? 

3. Имеется ли в последовательности 2, 4, 8, 16, 32, 64, 128, ... число, которое, как и 8,отличается от некоторой степени числа 10 на 2?

4. На бесконечном во все стороны листе клетчатой бумаги в каждой клетке записано натуральное число, причём все натуральные числа встречаются по одному разу. Докажите, что найдутся две клетки, имеющие общую сторону, числа в которых различаются больше чем на миллиард.

5. Одиннадцать вершин правильного25-угольника отмечены красным цветом. Обязательно ли найдутся три отмеченные точки, которые являются вершинами некоторого равнобедренного треугольника?