«Квант» для «младших» школьников Задачи 1973 года

«Квант» для «младших» школьников

Задачи первого номера 1973 года

1. Двое приятелей не виделись много лет. Встретившись, они разговорились, и один похвалился другому, что у него уже трое детей. «Сколько же им лет?»,— спросил второй. «Произведение их лет равно 36, а сумма — номеру вот этого трамвая». Посмотрев на номер трамвая, второй собеседник сказал, что этих данных недостаточно. «А старший сын у меня рыжий»,— «Тогда я знаю, сколько им лет»,— сказал его приятель и точно назвал возраст каждого ребёнка. Сколько же лет было каждому ребёнку?

2. На очередном занятии математического кружка каждый школьник получил 8 карточек с числами. Требовалось разложить карточки в две строчки (по 4 карточки в строчку) так, чтобы суммы чисел строчек были равны между собой. Один из играющих разложил карточки в одну строчку так, как показано на рисунке, и немедленно заявил комиссии, что задача не имеет решения. Почему ученик, не занимаясьподробным подсчётом, сделал такое заявление? И как всё-таки решить задачу?

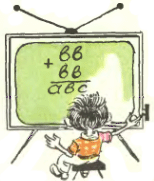3. Расшифруйте пример на сложение. 

4. Переверните нераспечатанную бутылку кефира и постучите по донышку так, чтобы брызнул кефир (для осторожности, проделайте все это над глубокой тарелкой). Что сделалось с крышкой и почему?

5. Два человека несут бревно, поддерживая его на одинаковых расстояниях от концов. Третий, желая помочь, берётся за бревно впереди первого. Будет ли легче несущим бревно? (Или: что скажет второй?)

Задачи второго номера 1973 года

1. Мышке до норки 20 шагов. Кошке до мышки 5 прыжков. Пока кошка совершает один прыжок, мышка делает 3 шага; а один кошачий прыжок равен по длине 10 мышинымшагам. Догонит ли кошка мышку?

2. Как можно измерить высоту телеграфного столба, имея в своем распоряжении только небольшую линейку? (На столб залезать нельзя.)

3. Найдите наименьшие натуральные числа а, b (где b > 1), для которых квадратный корень из произведения числа aи квадратного корня из произведения числа a на квадратный корень из числа a равен числу b.

4. Канал представляет собой жёлоб, установленный на сваях. Меняется ли сила давления на сваи, когда по каналу тянут баржу?

5. На прямой через равные промежутки поставили 10 точек, они заняли отрезок длины l. На другой прямой через такие же промежутки поставили 100 точек, они заняли отрезок длины L. Во сколько раз L больше, чем l?

6. По шоссе со скоростью 100 км/ч движутся машины. При этом расстояние между машинами, идущими друг за другом, около 15 м. Можно ли потребовать, чтобы на более узком участке для обеспечения безопасности скорость машин понижалась до 15 км/ч?

Задачи третьего номера 1973 года

1. Электропоезд длиною 18 м проезжает мимо километрового столба за 9 секунд. Сколько времени ему понадобится, чтобы проехать мост длиной 36 м?

2. У двух продавцов было по 30 яблок у каждого. Первый продавал по 2 яблока за 1 рубль, второй — по 3 яблока за1 рубль. Во время торговли одного вызвали домой, и он попросил второго продавца продать его яблоки. Оставшиеся яблоки второй продавец продавал по 2 рубля за 5 яблок. Если бы они продавали порознь, то получили бы 10 + 15 = 25 рублей, а продавая 5 яблок по 2 рубля, они получили лишь 24 рубля.Куда делся рубль?

3. Волк заметил зайчонка в двадцати метрах, когда тому до спасительного леса оставалось 250 м. Зайчиха-мать, желая отвлечь преследователя от детёныша, перебегает дорогу волку перед самым носом. Волк остановился в нерешительности,не зная, чему отдать предпочтение — количеству или качеству мяса. Лишь одна секунда понадобилась волку, чтобы принять правильное решение. Какое решение должен был принять волк и какой вывод сделать, если скорость зайчонка 540 м/мин,волка — 600 м/мин, а скорость зайчихи не меньше скорости волка?

4. Корабль переходит из реки в море. Меняется ли при этом его осадка?

Задачи четвёртого номера 1973 года

1. Найдите наименьшие натуральные числа a и d,удовлетворяющие равенству 500a — 7d = 1.

2. Когда наливают сок из жестяной банки через отверстие в крышке, то делают два отверстия. Только тогда идёт хорошая струя. Почему?

3. Мой дед старше моего отца на 32 года, а мой отец на столько же старше меня. Сколько сейчас лет каждому из нас, если три года тому назад нам всем вместе не было и ста лет?

4. На столе лежит стопка книг. Что легче: вытянуть нижнюю книгу, придерживая (но не приподнимая!) остальные, или привести в движение всю стопку, потянув за нижнюю книжку? 

5. Восстановите пример на умножение 38,? · ?6 = ???, заменив вопросительные знаки на цифры, не равные нулю.

6. В цепи, содержащей электрическую лампочку, сопротивления подводящих проводов и нити лампы одинаковы, однако нить накаляется добела, а провода почти не нагреваются. Почему?

Задачи пятого номера 1973 года

1. При любом натуральном n число 6⁴ⁿ⁺² – 2ⁿ⁺³ · 3ⁿ⁺² + 36 делитсяна 900. Докажите это.

2. В одном из двух больших непрозрачных сосудов керосин, вдругом — керосин с водой. Придумайте способ различить эти сосуды, имея в своём распоряжении динамометр и гирьку на верёвочке.

3. Все натуральные числа от 1 до 100 разбиты на две группы: чётные и нечётные числа. В какой из групп сумма всех цифр, использованных для записи чисел, больше? На сколько?

4. Автомобиль едет со скоростью 60 км/ч. С какой скоростью должен ехать другой автомобиль, чтобы проходить каждый километр на 2 минуты быстрее? На 1 минутубыстрее? Вообще, на сколько быстрее может проходить второй автомобиль 1 километр?

5. Восстановите формулу, если после замены цифр на цветные звёздочки (каждаяцифра — своей звёздочкой) получается такой рисунок: 

6. Почему ручки к дверям привинчивают у «свободного» края?

Задачи шестого номера 1973 года

1. В кружках треугольника на рисунке справа были расставлены все числа от 1 до 7(каждое по одному разу), причём сумма чисел вдоль каждого отрезка прямой была одна и та же. Определите, какое число было записано в вершине треугольника и чему равнялись указанные суммы.

2. В трёх сообщающихся сосудах находится вода. Левый сосуд открыт. Одинаково ли давление в точках A, B и C, если они лежат на одной горизонтали?

3. На рисунке изображена фигура в виде буквы Т с четырьмя отмеченными клетками. Разделите эту фигуру по линиям сетки на четыре конгруэнтные части так, чтобы в каждой из частей было по одной отмеченной клетке.

4. Прыгать с обрыва в песок безопаснее, чем на твёрдую землю. Почему?

5. Объясните равенства 19 = 1 · 9 + (1 + 9), 29 = 2 · 9 + (2 + 9), 99 = 9 · 9 + (9 + 9), 109 = 10 · 9 + (10 + 9),1239 = 123 · 9 + (123 + 9) и так далее.

6. Деревянный и чугунный бруски по отдельности уравновешивались в воздухе десятикилограммовой гирей. Что произойдёт, если бруски положить на разные чашки весов, а весы поместить под стеклянный колпак и откачать воздух?

Задачи седьмого номера 1973 года

1. У двух рыбаков спросили: «Сколько рыбы в ваших корзинах?» «В моей корзине половина числа рыб, находящихся в корзине у него, да ещё 10»,— ответил первый.«А у меня в корзине столько рыб, сколько у него, да ещё 20»,— сказал второй. Сколько же рыб у первого, а сколько у второго?

2. Ветер уносит воздушный шар в северном направлении. В какую сторону при этом отклоняется флажок, прикреплённый к вершине гондолы?

3. К треугольнику на рисунке пристроили равнобедренный треугольник так, что получился новый треугольник. Сколькими способами это можно сделать?

4. Даны два совершенно одинаковых длинных железных стержня. Один из них намагничен. Определите, какой из двух стержней намагничен, не пользуясь никакими другими предметами.

5. В кладовке я нашёл кусок фанеры прямоугольной формы, расчерченный на 64 клетки.«Хорошо бы из неё сделать шахматную доску»— подумал я. Но как? Помогите мне разрезать этот кусок фанеры на 2 части так, чтобы из них можно было склеить шахматную доску.

Указание   Ответ

6. Из таящего снега снежки лепить легко, а когда температура снега намного ниже нуля градусов Цельсия, снежки лепятся очень плохо. Почему?

Задачи восьмого номера 1973 года

1. Даны два последовательных натуральных числа a и b, а также их произведение c.Докажите, что число a² + b² + c² является квадратом некоторого нечётного числа.

2. Электрик, монтажник и инженер, фамилии которых Бауманн, Эйхлер и Хаан (не обязательно в таком порядке!), летели рейсом из Праги в Каир. Из разговора, который они вели в самолете, выяснилось, что:

• Бауманн и инженер собирались работать на строительстве;
• электрик и Хаан живут постоянно в Берлине;
• Эйхлер моложе, чем монтажник;
• Хаан старше, чем инженер.

Назовите фамилии инженера и электрика (ответ нужно обосновать!).

3. Поезд проходит по мосту длиной 171 м за 27 с (считая от момента въезда на мост локомотива до ухода последнего вагона), а мимо пешехода, идущего навстречу поезду со скоростью 1 м/с,— за 9 с. Найдите скорость поезда и его длину.

4. Катер проходит путь от A до B вверх по течению за 4 часа 30 минут, а путь от B до A (вниз по течению) — за 3 часа. Сколько времени будет плыть от B до A плот?

5.Во время стоянки между двумя рейсами матросу исполнилось20 лет. По этому случаю в кают-компании собрались все 6 членовкоманды.
— Я вдвое старше юнги и на 6 лет старше машиниста,— сказал рулевой.
— А я на столько же старше юнги, на сколько моложе машиниста,— заметил боцман. — Кроме того, я на 4 года старше матроса.
— Средний возраст команды — 28 лет,— дал справку капитан.
Сколько лет капитану?

Задачи девятого номера 1973 года

1. В примере на сложение цифры были заменены буквами (одинаковые — одинаковыми, разные — равными). Получилось вот что: УДАР + УДАР = ДРАКА. Расшифруйте этот пример.

2. Семиклассник Петя переехал в новый пятиэтажный дом, у которого 1-й и2-й этажи во 2-м и 3-м подъездах заняты под магазин. Все лестничные площадки дома устроены одинаково, на каждой из них находится не более четырёх квартир. Петя живёт в 31-й квартире. На каком этаже живёт Петя?

3. На верёвочной петле в горизонтальном положении висит палка, один конец которой значительно толще другого. Палку разрубили в том месте, где была петля. Одинаковы ли массы полученных частей?

4. Почему трещат горящие дрова?

5. Если машинист не может сразу сдвинуть с места тяжёлый состав, он даёт сначала задний ход, а затем медленно трогает состав с места. В чём тут дело?

Задачи десятого номера 1973 года

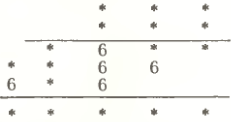1. Расшифруйте умножение.

2. У велосипеда есть передний и задний тормоза.В каком порядке их нужно включать при резкой остановке?

3. Я и мой друг приобрели за 3 дня 18 марок. Сегодня я купил столько марок, сколько мой друг вчера и сегодня, но зато позавчера он купил на 2 марки больше, чем я вчера и позавчера. Сколько же марок приобрёл каждый из нас?

4. Что произойдёт, если включённый электронагреватель вынуть на некоторое время из воды? (Ни в коем случае не делайте это! Задача исключительно теоретическая, опыт приведёт к беде!!!)

5. В кузове грузовой машины оставили бревно с гвоздём в середине. Бревно при движении машины свободно каталось в кузове и царапало дно. Какая часть дна кузова может быть испорчена? Размеры кузова — 3 на 2 метра; длина бревна — 2 м.

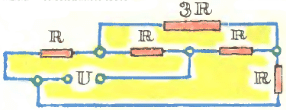6. Какой ток идёт через сопротивление 3R в схеме, показанной на рисунке? Величины всех сопротивлений и напряжение U считайте известными.

Задачи одиннадцатого номера 1973 года

1. Фигуристка, вращаясь при парном катании вокруг своей оси, 20 раз повернулась лицом к своему партнёру, который за те же 10 секунд сделал два оборота вокруг фигуристки. Сколько оборотов в секунду выполняла фигуристка?

2. Почему трудно прыгнуть на берег с лёгкой лодки?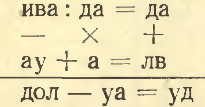

3. Расшифруйте пример, где цифры зашифрованы буквами.

4. Чтобы снег на тротуарах скорее таял, его посыпают солью. С другой стороны, для получения низких температур снег смешивают с солью в отношении две весовые части к одной весовой части. Таким образом, соль в первом случае способствует нагреванию, а во втором —охлаждению. Нет ли здесь противоречия? 

5. От необитаемого острова отошла лодка, на создание которой у Робинзона ушло 20 лет. На плече у Робинзона сидел любимец-попугай. Вот что он иногда произносил:
— Хватайся за меня! Мы выплывем на берег. Слушай меня, ведь я втрое старше тебя.
— Ещё ни один корабль не подошёл к нам. Надо самим строить лодку.
— Море-то я хорошо знаю. Ведь я прожил две твои жизни.
— Крепи весло! Мы ещё погуляем по большой земле, хоть мне лет в полтора раза больше, чем тебе.
Сколько лет попугаю? Сколько лет провёл Робинзон на острове?

Задачи двенадцатого номера 1973 года

1. Гриша пошёл с папой в тир. Уговор был такой: Гриша делает пять выстрелов и за каждое попадание в цель получает право сделать ещё два выстрела. Всего Гриша сделал17 выстрелов. Сколько раз Гриша попал в цель?

2. Почему грязный, покрытый копотью снег тает быстрее, чем чистый?

3. Сашина комната обладает таким свойством: если её «поставить на бок» (на любую из боковых стен), то её площадь не уменьшится. Высота потолка комнаты равна 3 метрам.Какова наибольшая возможная площадь такой комнаты?

4. Металлический лист с дырочкой нагревают. Как меняется при этом размер дырочки?

5. В семье четверо детей. Им 5, 8, 13 и 15 лет. Детей зовут Аня, Боря, Вера и Галя. Сколько кому лет, если одна девочка ходит в детский сад, Аня старше Бори, а сумма возрастов Ани и Веры делится на три?

6. Судно массы m переместилось вверх по течению реки, поднявшись при этом на высоту h. Нужно ли при вычислении работы, совершённой двигателем, учитывать величину mgh?