«Квант» для «младших» школьников Задачи 2004 года

«Квант» для «младших» школьников

Задачи первого номера 2004 года

1. В стране Гдетотамии на пост президента претендуют два кандидата: Любимчик Джо и Зазнайка Билл. Каждый гражданин Гдетотамии может проголосовать за любого из них либо против всех. Побеждает тот из кандидатов, кто набирает больше голосов. В день выборов избирательная комиссия проверила 60% бюллетеней проголосовавших граждан. Убедившись, что 80% голосов в этих бюллетенях отданы за Любимчика Джо, а 10% — за Зазнайку Билла, комиссия отказалась от дальнейшего подсчёта голосов и объявила президентом Гдетотамии Любимчика Джо. Не поторопилась ли она со своим выводом?

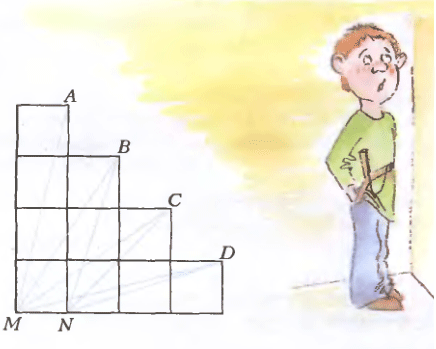2. На клетчатой бумаге нарисованы углы MAN, MBN, MCN и MDN. Докажите, что сумма их величин равна 45°. 

3. Для какого наибольшего числа n можно расставить на шахматной доске коней так, чтобы каждый конь бил ровно n других?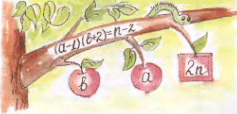

4. У натурального числа n есть такие различные натуральные делители a и b, что

(a – 1)(b + 2) = n – 2.

Докажите, что 2n — квадрат натурального числа. 

5. В коллективе n сотрудников. Каждые двое из них либо друзья, либо враги, причём у каждого сотрудника ровно 3 врага. Каждый сотрудник может правдиво заявить: «Враги моих друзей — мои враги». При каких n такое возможно?

Задачи второго номера 2004 года

1. Три математика ехали в разных вагонах одного поезда. Подъезжая к станции, они стали подсчитывать скамеечки на привокзальном перроне. У них получилось 15, 12 и 7 скамеечек. Отъезжая от станции, математики принялись считать заново, причём один из них насчитал скамеечек в три раза больше, чем другой. А сколько насчитал третий?

2. В записи десятизначного числа использованы все 10 цифр.Двигаясь слева направо, вместо каждой цифры этого числа записали количество цифр, которые меньше неё и расположены справа от неё. Получили 3 501 210 210. Каким было первоначальное число?

Ответ

3. — Над чем задумались, Ватсон?
— Я никак не могу понять, как разделить дугу салфетки, имеющей форму четверти круга, на три равные части. Проблема в том, что у меня нет с собой никаких чертёжных инструментов!
— Они вам не понадобятся, Ватсон. Чтобы справиться с этой задачей, достаточно лишь ваших рук.
— Ох, неплохо было бы иметь ещё и голову!
Помогите Ватсону справиться с его задачей. 

4. Три числа таковы, что их сумма больше нуля, а сумма их кубов меньше нуля. Могут ли ровно два из этих чисел быть отрицательными? 

5. Отметьте 16 клеток шахматной доски так, чтобы не нашлось ни одного остроугольного треугольника с вершинами в центрах отмеченных клеток. А можно ли отметить 17 таких клеток?

Задачи третьего номера 2004 года

1. Придумайте хотя бы один способ заменить буквы цифрами (разные буквы —разными цифрами, одинаковые — одинаковыми) так, чтобы выполнялись равенства

Д + О + К + Т + О + Р = А + Й + Б + О + Л + И + Т,

Д · О · К · Т · О · Р = А · Й · Б · О · Л · И · Т.

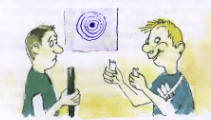2. Два спортсмена соревнуются в точности стрельбы (точностью стрельбы называют отношение числа успешных выстрелов к числу использованных патронов). Вначале каждому спортсмену выдают 20 патронов. Соревнование проходит в два этапа, причём на каждом этапе спортсмен может использовать любую отличную от нуля часть патронов. Могла ли на каждом из двух этапов точность стрельбы первого спортсмена быть выше точности стрельбы второго, а по общему результату соревнований точность стрельбы первого спортсмена быть ниже точности стрельбы второго?

3. Число 2 100 010 006 интересно тем, что его первая цифра равна количеству единиц в этом числе, вторая —количеству двоек, ...., десятая — количеству нулей. А существует ли такое девятизначное число, у которого первая цифра равна количеству НЕ единиц, вторая — количеству НЕ двоек, ..., девятая — количеству НЕ девяток?

4. Круг накрывает половину периметра правильного шестиугольника. Может ли при этом шестиугольник накрывать половину периметра круга? 

5. В лесу водятся крикливые пушистые зверюшки, среди которых имеются барабашки. Какого бы зверя ни взять, существует барабашка точно такой же крикливости и существует барабашка точно такой же пушистости (возможно, это один и тот же барабашка). Среди зверюшек одинаковой крикливости барабашки самые пушистые. Среди барабашек более крикливые являются более пушистыми. Следует ли отсюда, что среди всех зверюшек одинаковой пушистости барабашки наименее крикливые?

Задачи четвёртого номера 2004 года

1. Каких натуральных чисел от 1 до 10000 больше: чётных или нечётных с чётной суммой цифр?

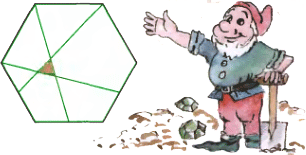2. В правильном шестиугольнике три последовательные вершины соединены с серединами соответствующих сторон. Докажите, что в пересечении образовался равносторонний треугольник.

3. Двор императора погряз в интригах.Но самым ловким интриганом оказался сам император. Он разведал состав всех действующих при дворе тайных обществ, и оказалось, что в каждом из них состоят ровно трое придворных. Каждый день всех придворных, состоящих на начало этого дня в наибольшем числе обществ, император стал ссылать на повышение в провинцию. Общества, понёсшие потери в составе, распадаются, а новые указы о повышениях издаются до тех пор, пока не распадутся все общества.
Хранитель Императорской чернильницы состоит в меньшем числе тайных обществ, чем кто-либо другой из придворных, и поэтому пребывает в уверенности, что его никуда не сошлют. Обоснована ли эта уверенность, если состав остальных обществ хранителю неизвестен?

4. Пять натуральных чисел таковы, что наибольший общий делитель любых трёх из них равен наименьшему общему кратному оставшихся двух. Могут ли среди этих чисел быть неравные?

5. Прямолинейный канал, имеющий ширину 1, дважды поворачивается под прямым углом так, как показано на рисунке. Расстояние между участками поворота достаточно велико. Очевидно, что по этому каналу может проплыть квадратный плот площади 1. Укажите плот ещё большей площади, который тоже сможет проплыть по каналу.

Задачи пятого номера 2004 года

1. Больному прописали таблетки двух сортов А и Б, не отличающиеся по внешнему виду. Через определённые промежутки времени он должен одновременно принимать одну таблетку сорта А и одну таблетку сорта Б, в любых других сочетаниях лекарств для больного наступают нежелательные последствия. Когда до окончания курса лечения ему осталось принять 4 таблетки(2 таблетки сорта А и 2 таблетки сорта Б), он их случайно перемешал. Присутствовавший при этом математик его успокоил, сказав, что можно благополучно завершить лечение, не подвергнув здоровье риску. Что для этого нужно сделать?

2. В ряд выложили дукаты и цукаты, не отличающиеся по внешнему виду. Каждый дукат весит 7 граммов, а каждыйцукат — 8 граммов. Как с помощью только двух взвешиваний на чашечных весах без гирь отделить дукаты от цукатов, если известно, что любой цукат лежит правее каждого дуката, а всего в ряд выложили 10 предметов?

3. Последовательность натуральных чисел строится следующим образом. Первое число равно 1. Каждое следующее число получается из предыдущего умножением на 2 и прибавлением к результату 1. Сколько среди первых 2004 членов этой последовательности чисел, делящихся на 5?

4. На шахматной доске расставлены белые и чёрные ферзи — поровну каждого цвета. При этом оказалось, что ферзи одного цвета не угрожают друг другу. Каково наибольшее возможное число ферзей?

5. В окружность вписали квадрат, а затем четыре дуги окружности симметрично отразили относительно стягивающих их хорд. Малыш утверждает, что в результате получилась фигура, показанная на левом рисунке (дуги пересекаются только в вершинах квадрата). Карлсон же убеждён, что получится фигура, показанная на правом рисунке (дуги пересекаются также и в других точках). Кто из них прав?

Задачи шестого номера 2004 года

1. В редакцию журнала «Квант» пришло электронное письмо в странной кодировке:

«ъДТБЧУФЧХКФЕ!
рПУЩМБА ЪБДБЮХ ДМС МЕФОЕЗП ФХТОЙТБ 6-8».

Помогите его расшифровать.

2. Могут ли 6 футболистов расположиться на футбольном поле так, чтобы каждый из них мог дать пас по земле ровно четырём другим? 

3. Найдите наименьшее составное число, которое не делится ни на одно из натуральных чисел от 2 до 100.

4. Ненулевые числа x, y и z таковы, что

x² – y² = yz

и

y² – z² = xz.

Докажите равенство

x² – z² = xy.

5. С крыши дома на землю спущена лестница. На каждой её ступеньке укреплен указатель-стрелка, направленный либо вверх, либо вниз. В начальный момент на одной из ступенек лестницы стоит человек. Далее он передвигается на соседнюю ступеньку в соответствии с указателем, после чего этот указатель меняет направление на противоположное. Со следующей ступеньки человек опять переступает на соседнюю в соответствии с её указателем, после чего этот указатель тоже меняет положение на противоположное. Далее он снова и снова переходит со ступеньки на ступеньку по таким же правилам. Докажите, что при любых начальных направлениях стрелок и любом исходном положении человек рано или поздно сойдёт с лестницы либо на крышу, либо на землю.