«Квант» для «младших» школьников Задачи 2000 года

«Квант» для «младших» школьников

Задачи первого номера 2000 года

1. Д'Артаньян сообщает Атосу, Портосу и Арамису три цифры, из которых мушкетёры составляют трёхзначные числа. Может ли д'Артаньян подобрать цифры таким образом, чтобы все три числа, составленные Атосом, Портосом и Арамисом, были простыми?

Ответ   Решение

2. У шестиклассника 10 предметов. За год его среднийбалл 4,6. Сколько у него троек, четвёрок и пятёрок, если известно, что есть все эти оценки, а двоек никомуне ставят?

3. Для физических опытов в мастерской должны были изготовить 10 стеклянных шариков: два красных, два синих, два жёлтых, два зелёных и два белых. Все шарики должны были иметь одинаковую массу. Однако изготовители допустили ошибку, и два шарика одного цвета оказались на 1 грамм легче, чем следовало.
В нашем распоряжении имеются точные аптечные весы с двумя чашками и набором гирь-разновесов, позволяющие точно определить, на сколько граммов содержимое одной чашки легче или тяжелее другой. Можно ли с помощью единственного взвешивания определить, шарики какого цвета легче других?

Ответ   Указание   Решение

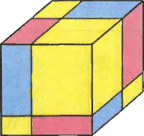4. Три плоскости, параллельные граням куба, рассекают каждую из видимых граней на четыре прямоугольника. Что больше: сумма площадей красных прямоугольников или сумма площадей синих прямоугольников?

5. Постройте замкнутую ломаную линию, которая каждое свое звено пересекает ровно один раз, причём под прямым углом.

Задачи второго номера 2000 года

1. Расставьте вместо букв цифры, если разные буквы обозначают разные цифры:

ГАММА + СИГМА = ЛАМБДА.

2. Убедитесь, что число, десятичная запись которого начинается цифрой 2,заканчивается цифрой 3, а остальные 100 цифр — пятёрки, является составным.

Решение

3. Для съёмок музыкального клипа группа «Егорушки International» собирала в мешки тополиный пух. Саша собрал более половины всех мешков — в 5 раз больше, чем Валера, и на 10 мешков больше, чем Андрей. Возмущённый такой несправедливостью, Валера отобрал у каждого из приятелей несколько мешков, так что у всех троих мешков стало поровну. Сколько всего мешков пуха собрали «Егорушки International»? 

4. Прямоугольное поле расчертили на клетки линиями, параллельными его сторонам.В каждую клетку этого поля встало по одному танцору, которые предварительно взялись за руки, образуя замкнутую цепочку. Каждые два соседних танцора оказались на клетках, имеющих общую сторону. Может ли поле состоять из 1001 клетки?

Ответ   Указание

5. Маша старается выпекать лепёшки в форме параллелограммов, но у неё получаются лишь изделия в форме выпуклых четырёхугольников, не являющихсяпараллелограммами. Утешая её, Даша утверждает, что из каждой такой лепёшки можно вырезать параллелограмм, три вершины которого совпадут с вершинами четырёхугольника. Права ли Даша?

Задачи третьего номера 2000 года

1. Алёша на 3 года старше Бори и на 6 лет старше Вовы. Произведение возрастов Гриши и Бори на 9 больше произведения возрастов Алёши и Вовы. На сколько лет Алёша старше Гриши?

2. «Будьте взаимно просты»,— сказал Умный Портняжка и разрезал ленту, на которой были написано число 123456789, на несколько частей так, что числа на каждых двух отрезанных кусках оказались взаимно простыми. Какое наибольшее количество кусков ленты могло при этом получиться?

3. Существует ли такое натуральное число n, что n² + n + 1 делится на 9?

4. На острове Рыцарей и Лжецов живут только рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. В Думе острова 101 депутат. В целях сокращения бюджета было решено сократить Думу на одного депутата. Каждый из депутатов заявил, что если его выведут из состава Думы, то среди оставшихся 100 депутатов большинство будет лжецами. Сколько рыцарей и сколько лжецов в Думе?

5. Стороны вписанного в квадрат четырёхугольника отсекают от квадрата 4 треугольника равной площади. Докажите, что вписанный четырёхугольник — тоже квадрат.

Задачи четвёртого номера 2000 года

1. В ящике лежат зелёные, жёлтые и красные яблоки трёх сортов. Может ли зелёных яблок быть больше, чем яблок первого сорта, яблок первого сорта больше, чем жёлтых яблок, жёлтых яблок больше, чем яблок второго сорта, яблок второго сорта больше, чем красных яблок, а красных яблок больше, чем яблок третьего сорта?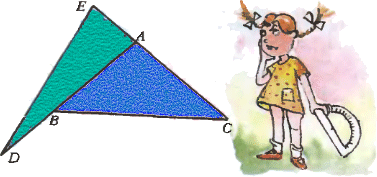

2. Угол BACравнобедренного треугольника ABCтупой. На луче ABвзята точка D, а на луче CA — точка Eтак, чтоAD = BC = CE.Докажите, что если треугольник DAE равнобедренный, то величина угла ВАС равна 100°.

3. В девяти клетках таблицы 3×3 которой записаны все натуральные числа от 1 до 8 и ещё число x так, что сумма чисел в каждой строке и в каждом столбце одна и та же. Найдите число x.

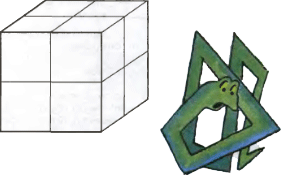4. На поверхности клетчатого куба 2×2×2 нарисована замкнутая несамопересекающаяся ломаная, каждое звено которой является стороной какой-либо клетки. Могут ли на этой ломаной оказаться все вершины куба, все центры граней куба и все середины его рёбер?

5. Пончик поспорил с Сиропчиком, что за 25 минут съест больше пирожков, чем Сиропчик выпьет стаканов лимонада. За каждую минуту Пончик съедает 4 или5 пирожков, а Сиропчик выпивает 3 или 6 стаканов лимонада. Через 10 минут после старта Сиропчик обогнал Пончика на 20%, но за 4 следующие минуты Пончик неимоверными усилиями сравнял счёт. Ещё через 6 минут уже Сиропчик отставал от Пончика на 10%, но в конце концов всё-таки сумел одержать победу. Сколько съел (выпил) каждый?

Задачи пятого номера 2000 года

1. — Сколько раз вы объявили шах?— спросили у гроссмейстера после окончания игры.
— А вы сами узнаете, если я скажу, что в цифровом ребусе

ШАХ + ШАХ + ... + ШАХ = МАТ

слово ШАХ встречается столько раз, сколько я объявил шах во время партии, причём количество чисел, зашифрованных словом ШАХ, здесь наибольшее,— ответил тот.
Сколько же?

2. Бивис и Батт-Хед смотрели три программы видеоклипов по трём телевизорам одновременно. Первая программа содержала в полтора раза меньше клипов, чем вторая, а всего в трёх программах было 200 клипов. Из всего просмотренного Бивису понравилась лишь пятая часть клипов первой программы и половина клипов второй программы. Батт-Хеду понравилось столько же клипов, сколько и Бивису, в том числе все клипы третьей программы. А сколько клипов им не понравилось?

3. В некотором городе на любом перекрёстке сходятся ровно три улицы. Улицы раскрашены в три цвета так, что на каждом перекрёстке сходятся улицы трёх разных цветов. Из города выходят три дороги. Обязательно ли эти дороги разных цветов?

4. Имеется 100 карточек. Какие бы 50 из них ни взять, среди них можно выбрать 30 таких, что какие бы 20 из них ни взять, из них можно выбрать 10 таких, что какие бы 5 из них ни взять, среди них окажется не менее 3 красных карточек. В то же время, какие бы 80 карточек из 100 ни взять, среди них можно выбрать 20 таких, что какие бы 10 из них ни взять, среди них окажется не менее 2 синих карточек. Сколько красных и сколько синих карточек находится в колоде?

5. Когда жители Параллелограммии отвоевали у жителей Пентагонии пятиугольный участок поля, они решили разделить его на участки в виде параллелограммов. Удастся ли им это сделать?

Задачи шестого номера 2000 года

1. В математическом примере зашифровано слово из десяти разных букв, которое обозначает название космического корабля будущего. Определите числовое значение каждой буквы, затем напишите последовательно цифры от 0до 9, а под ними — соответствующие им буквы, и вы прочтёте искомое слово.

2. Два четырёхзначных числа a и b написаны одними цифрами, но в разном порядке. Может ли сумма цифрчисла a равняться сумме цифр числа a + b?

3. Из четырёх палочек сложен четырёхугольник, диагонали которого перпендикулярны. Докажите, что из них можно сложить четырёхугольник с двумя прямыми углами. 

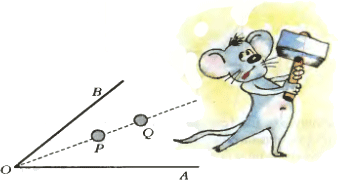4. В остром угле AOB между двумя стенками геометрического бильярда расположены два шара Р и Q на одном луче, проходящем через точку О. Если шар Р ударить так, что он, отскочив последовательно от стенок АО и ВО, столкнётся с шаром Q, то пройденное им расстояние будет таким же, как если его ударить так, что он, отскочив последовательно от стенок ВО и АО, столкнётся с шаром Q. Докажите это.

5. В пробирке находились бактерии и вирусы общей численностью 2000 штук. Сначала каждая бактерия убила по три вируса, затем каждый оставшийся вирус уничтожил по две бактерии, после чего опять каждая оставшаяся бактерия убила по три вируса, затем каждый оставшийся вирус уничтожил по две бактерии... Такой «обмен ударами» продолжался до тех пор, пока бактерий и вирусов не оказалось поровну. Сколько же их осталось?