«Квант» для «младших» школьников Задачи 1980 года

«Квант» для «младших» школьников

Задачи первого номера 1980 года

1. Из двадцати мальчиков нашего класса у четырнадцати — карие глаза, у пятнадцати —тёмные волосы. Семнадцать мальчиков весят больше 40 кг, а 18 мальчиков выше 1 м 60 см.Докажите, что по крайней мере четверо мальчиков обладают всеми перечисленными признаками.

2. Если из некоторого числа вычесть 7, а остаток умножить на 7, то получится тот же результат, как если бы мы вычли из данного числа 11, а остаток умножили на 11. Найдите это число.

3. Имеется 5 листов бумаги. Некоторые из них порвали на5 кусков каждый. Некоторые из полученных кусков снова порвали на 5 частей, и так далее. Можно ли, продолжая эту операцию, получить 1980 листочков? 

4. Имеется некоторое количество гирь, массы которых не превосходят 10 кг. При любом разбиении всех гирь на две кучки масса хотя бы одной из кучек не превосходит 10 кг.Найдите наибольшую возможную общую массу всех гирь.

5. Расшифруйте ребус ПС^И = ИКС.

6. Четырёхзначное число X является квадратом двузначного числа Y. Четырёхзначное число, полученное чтением десятичной записи числа X справа налево, является квадратом некоторого двузначного числа, кратного числу Y.Найдите числа X и Y.

7. Имеет ли уравнение

x² + y² + z² = 1980

решение в целых числах?

Задачи второго номера 1980 года

1. а) Два натуральных числа отличаются на 2, а их квадраты — на 100. Какие это числа?

б) Квадраты двух последовательных натуральных чисел отличаются лишь перестановкой последних двух цифр. Найдите эти числа.

2. Для нумерации страниц книги потребовались 1392 цифры. Сколько в этой книге страниц?

3. На улице, став в кружок, беседуют Аня, Валя, Галя и Надя. Девочка в зелёном платье (не Аня и не Валя) стоит между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом платье и Валей. Какое платье носит каждая из девочек? 

4. Если головоломка, которую вы разгадали перед тем, как вы разгадали эту, была труднее, чем головоломка, которую разгадали после того, как разгадали головоломку, которую разгадали перед тем, как разгадали эту, то была ли головоломка, которую вы разгадали перед тем, как разгадали эту, труднее, чем эта?

5. Разрежьте параллелограмм по прямой, проходящей через его центр, так, чтобы из полученных двух кусков можно было сложить ромб.

Задачи третьего номера 1980 года

1. Два школьника пришли покупать себе буквари. Одномуне хватило семи копеек, другому — копейки. Они сложили свои деньги вместе, но всё равно денег не хватило. Сколько стоит букварь?

2. Можно ли на чёрных клетках шахматной доски расставить семь слонов (напоминаем: слон ходит по диагонали) так, чтобы они не били друг друга? А восемь таких слонов?

3. Прямоугольник делим прямой на два многоугольника. Затем один из них делим прямой на две части. Потом один из полученных трёх многоугольников вновь делим на две части, и так далее. Операцию разрезания многоугольников повторили 100 раз.Подсчёт показал, что у полученных многоугольников всего 302 вершины (вершины всех многоугольников считаем отдельно). Могло ли такое быть?

4. Вычислите 1 + 2 – 3 – 4 + 5 + 6 – 7 – 8 + 9 + 10 – 11 – 12 + 13 + 14 – ... + 301 + 302.

5. В квадратах на рисунках заполните пустые клетки буквами Н, О, Р, М, А так, чтобы в каждой строке, в каждом столбце и в каждой из двух диагоналей квадрата встречались все эти буквы, причём каждая по одному разу. Нельзя ли, заполнив клетки одного квадрата, получить заполнения остальных квадратов автоматически?

Задачи четвёртого номера 1980 года

1. Расшифруйте ребус, изображенный на рисунке (одинаковым буквам соответствуют одинаковые цифры, разным — разные). Затем, используя найденные значения букв, замените в записи

* О Л * И * М * П * И * А * Д * А * = 80

звёздочки арифметическими знаками, скобками или «пустым местом» (то есть уберите их) так, чтобы получилось верное равенство.

2. Разность 63! — 61! делится на 71. Докажите это. (Запись n! означает произведение всех целых чисел от 1 до n, например, 5! = 1 · 2 · 3 · 4 · 5.) 

3. Из шестнадцати спичек сложили пять квадратов, как показано на рисунке. Переложите две спички так, чтобы число квадратов уменьшилось на единицу.

4. В очереди за билетами в кино стоят друзья: Юра, Миша, Володя, Саша и Олег. Юра купит билет раньше, чем Миша, но позже Олега, Володя и Олег не стоят рядом, а Сашане рядом ни с Олегом, ни с Юрой, ни с Володей. Кто за кем стоит?

5. В какой системе счисления верно равенство10 + 10 = 10 · 10?

6. Равносторонний треугольник нетрудно разрезать на четыре равносторонних треугольника: достаточно соединить отрезками середины его сторон. Но можно ли разрезать егона 8, или 10, или 11 равносторонних треугольников? Вообще, на какое число равносторонних треугольников можно разрезать данный равносторонний треугольник?

Задачи пятого номера 1980 года

1. Из бумаги склеили куб. Очевидно, его поверхность можно разрезать на шесть конгруэнтных квадратов. Разрежьте её на двенадцать конгруэнтных квадратов.

2. На рисунке изображено родословное дерево одной семьи коми, родоначальником которой был некий Тихон Федорович. Вот все его потомки (на языке коми): Педот Тикбн, Остап Тикбн, Тикбн Вась, Педот Вась, Падей Остап, Тикбн Падей, Падей Ил-ля, Тикбн Педот. Известно, что среди них нет женщин. Установите, какое имя соответствует каждому узлу дерева.

3. Найдите два числа, разность и частное которых равны пяти. 

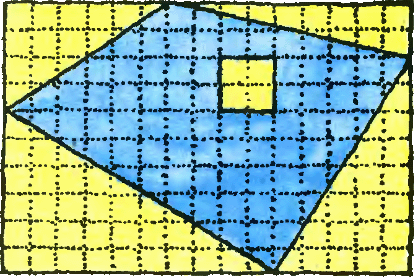4. Покажите, что площадь фигуры синего цвета равна половине площади прямоугольника. 

5. В книгах новгородских писцов XV века упоминаются такие меры жидких тел: бочка, насадка и ведро. Из этих же книг стало известно, что 1 бочка и 20 вёдеркваса уравниваются с тремя бочками кваса, а 19 бочек, 1 насадка и 15,5 ведрауравниваются с 20 бочками и 8 вёдрами. Можно ли на основании этих данных определить, сколько насадок содержится в бочке?

6. Рассмотрим трёхзначные числа, начинающиеся и оканчивающиеся одинаковой цифрой, например 343. Докажите, что если сумма первой и второй цифр делитсяна 7, то и все число делится на 7.

Задачи шестого номера 1980 года

1. У школьника было несколько монет достоинством в 15 и 20 копеек, причём двадцатикопеечных монет было больше, чем пятнадцатикопеечных. Пятую часть всех денег школьник истратил, заплатив две монеты за билет в кино. Половину оставшихся у него денег он отдал за обед, оплатив его тремя монетами. Сколько монет каждого достоинства было у школьника вначале?

2. Разрежьте квадрат на три части, из которых можно сложить тупоугольный треугольник.

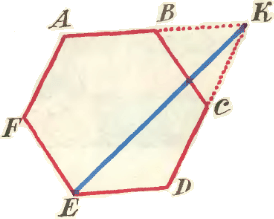3. Стороны AB и CD правильного шестиугольника ABCDEF продолжены до пересечения в точке K. Докажите, что квадрат длины отрезка EK в 7 раз больше квадрата длины отрезка AB. 

4. На карточках, изображённых на рисунке, написаны цифры. Сложите с их помощью четырёхзначное число, являющееся полным квадратом.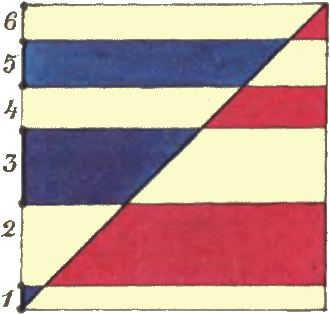

5. На стороне квадрата взято несколько точек так, что сумма длин первого, третьего и других отрезков с нечётными номерами совпадает с суммой длин второго, четвёртого и других отрезков с чётными номерами. Через взятые точки проведены прямые, параллельные другой стороне квадрата. Докажите, что сумма площадей синих «полосок» равна сумме площадей красных «полосок».

Задачи восьмого номера 1980 года

1. а) Найдите трёхзначное число, равное кубу суммы его цифр.
б) Найдите четырёхзначное число, равное четвёртой степени суммы его цифр.
в) Существует ли пятизначное число, равное пятой степени суммы его цифр?

2. Однажды я возвращался из воскресной поездки за город. В вагоне поезда было очень душно. Я вышел в тамбур, но и там было не лучше. Но вот поезд замедлил ход, и из щелей вентиляции подул свежий ветерок. Поезд остановился, ветерок затих, вновь возник во время следующего торможения, и так на всех станциях. Откуда он брался? В каком тамбуре вагона я находился —переднем или заднем? Замечу ещё, что дверь из тамбура в вагон и все окна в вагоне были открыты.

3. Можно ли из двадцати монет достоинством в 5, 20 и 50 копеек составить5 рублей?

4. За круглым столом сидят семь дипломатов. Они должны провести по одной беседе друг с другом. Два дипломата будут беседовать только в том случае, если окажутся рядом. После того как все дипломаты закончат переговоры со своими соседями, дипломаты встают и занимают новые положения для продолжения бесед.
Можно ли организовать встречу дипломатов так, чтобы при каждом новом размещении за столом у каждого из них были бы новые соседи?

5.Разделите круглый циферблат часов на три части так, чтобы сумма чисел в каждой части была равна 17.

Задачи девятого номера 1980 года

1. Первый и четвёртый члены последовательности равны 1, а второй, третий и пятыйравны –1. Шестой равен произведению первого на второй, седьмой — произведению второго на третий, восьмой — произведению третьего на четвёртый, и так далее. Найдите 1980-йчлен этой последовательности.

2. Из карточек, на которых написаны цифры, сложена фигура, изображённая на рисунке. Володя предложил Саше разложить карточки так, чтобы фигура осталась прежней, но каждая карточка касалась только новых соседей. Саша до сих пор решает эту задачу и никак не может её решить. Что вы ему посоветуете?

3. Если в январе четыре понедельника и четыре пятницы, то какой день недели — 1 января?

4. В стозначном числе

12345678901234567890123...7890

вычеркнули все цифры, стоящие на нечётных местах. В полученном пятидесятизначном числе вновь вычеркнули цифры, оказавшиеся на нечётных местах. Вычёркивали до тех пор, пока ничего не осталось. Какая цифра была вычеркнута последней?

5. Можно ли раскрасить клетки квадратной сетки 5×5 в пять цветов так, чтобы в каждой строке и в каждом столбце были клетки всех пяти цветов, а поля каждого цвета можно было обойти ходом шахматного коня, побывав на каждом из пяти таких полей ровно один раз?

Задачи десятого номера 1980 года

1. В примере на умножение одна из цифр заменена звёздочкой, а остальные — точками, как показано на рисунке. Сумма цифр четырёхзначного сомножителя равна 19. Восстановите пример.

2. На гипотенузе AB прямоугольного треугольника ABC от вершины A отложим отрезок AD, конгруэнтный катету AC, а от вершины B — отрезок BE, конгруэнтный катету BC. Докажите, что длина отрезка DE равна диаметру окружности, вписанной в треугольник ABC.

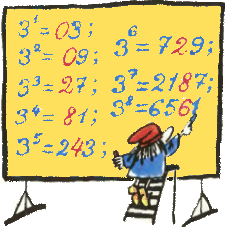3. Выпишем несколько первых степеней тройки. Получаются числа, у которых в разряде десятков —чётная цифра. Верно ли, что так будет всегда?

4. Доля блондинов среди голубоглазых больше, чем их доля среди всего населения. Верно ли, что доля голубоглазых среди блондинов больше, чем их доля среди всего населения?

5. Найдите трёхзначное число, которое при возведении в степень, показатель которой равен цифре его разряда сотен, даёт пятизначное число, первая цифра которого равна цифре, стоящей в исходном числе разряде десятков,вторая — той, что в исходном числе обозначала единицы, третья — на единицу меньше первой цифры исходного числа, четвёртая равна второй цифре исходного числа, наконец, последняя совпадает с последней цифрой исходного числа.

Задачи одиннадцатого номера 1980 года

1. На столе лежат четыре карточки. Известно, что на каждой карточке с одной стороны —буква, а с другой — натуральное число. Какие карточки необходимо и достаточно перевернуть, чтобы выяснить, истинно или ложно предложение «Если на одной сторонекарточки — гласная буква, то на другой — чётное число»? 

2. Четыре футбольные команды: «Старт», «Комета», «Ракета» и «Вымпел» — провели каждая с каждой по одному матчу. Судья изготовил таблицу, содержащую результаты их встреч. Машинистка отпечатала таблицу с образца и отдала её судье. Но оказалось, что печатная машинка (она была очень старая) почти ничего не отпечатала (смотрите рисунок). Судья помнил, что остальные матчи окончились со счётом 2:0, 1:1, 2:2, 3:1, 5:3. Помогите ему заполнить таблицу. (В графе «Мячи» слева записывают количество забитых мячей, справа — количество пропущенных мячей. За победу начисляют 2 очка,за ничью — по 1 очку.)

3. Даны 1980 последовательных натуральных чисел. Можно ли возвести каждое число в какую-нибудь чётную степень так, чтобы сумма полученных чисел была квадратом натурального числа?

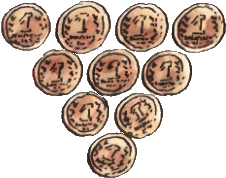4. Десять одинаковых монет образуют равносторонний треугольник, направленный вниз, как показано на рисунке. Переложите три монеты так, чтобы получился равносторонний треугольник, направленный вверх.

Задачи двенадцатого номера 1980 года

1. Заполните клетки нарисованного квадрата натуральными числами так, чтобы суммы чисел по каждой строке, каждому столбцу и диагоналям квадрата были одинаковыми (такие квадраты называются магическими) и равнялись 1980.

2. Что это за цифра, приписав которую в конце произвольного натурального числа, мы получим то же число, сложенное с этой цифрой и произведением данного числа на эту цифру?

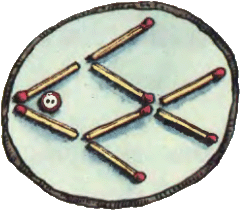3. Возьмите восемь спичек и пуговицу и сложите из них рыбку, как показано на рисунке. А теперь переложите три спички и пуговицу так, чтобы рыбка выглядела точно так же, но плыла в противоположном направлении.

4. По кругу записано больше трёх натуральных чисел, сумма которых равна 37. Суммы любых трёх последовательных чисел равны между собой. Какие числа записаны по кругу?

5. В будильнике, кроме часовой и минутной стрелок, есть ещё стрелка звонка. Часовщик построил механизм, с помощью которого эта стрелка равномерно двигается так, что всё время делит пополам угол между часовой и минутной стрелками. Сколько оборотов делает такая стрелка за сутки?