«Квант» для «младших» школьников Задачи 1999 года

«Квант» для «младших» школьников

Задачи первого номера 1999 года

1. Винни-Пух и Пятачок сели за стол немного подкрепиться и начали одновременно есть мёд из одного горшка,не отвлекаясь на разговоры. Если бы Винни Пух ел со скоростью Пятачка, то процесс еды длился бы на 4 минутыдольше, а если бы, наоборот, Пятачок ел со скоростью Винни-Пуха, то сократился бы на 1 минуту. За какое время мёд был полностью съеден?

2. На рынке продавали раков: больших — по 5 рублей, маленьких — по 3 рубля, а жаб — по рублю. Иван и Степан купили себе раков на одинаковые суммы денег, причём Иван купил больших и маленьких раков поровну, а Степан —вдвое меньше больших раков, чем маленьких. Иван расплатился одной сторублёвой купюрой, а Степан —несколькими десятирублёвыми. У продавца не оказалось мелких денег, поэтому он выдал сдачу Ивану опять же раками, а Степану — жабами. Сколько всего животных унесли приятели с рынка?

Ответ   Указание   Решение

3. Изображённый на рисунке на клетчатой бумаге шестиугольник разрежьте на три части, из которых можно сложить квадрат.

4. Я задумал натуральное число, которое записывается так же, как и число, которое я задумал, в системе счисления с основанием, равным числу, которое я задумал. Какое число я задумал?

Ответ

5. Кто из пиратов должен повернуться, чтобы узнать, верно ли утверждение: «Если у пирата есть серьга или косичка, то у него выбит глаз»?

Ответ

Задачи второго номера 1999 года

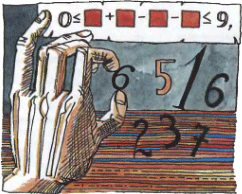1. Любые четыре цифры можно так распределить на две пары, что сумма цифр одной из них будет не более чем на 9 отличаться от суммы цифр второй пары. Докажите это.

2. — Я задумала такое число, — объявила Синеглазка, — что если к нему прибавить сумму его цифр, то получится 2000.
— А я задумал такое число,— похвастался Незнайка,— что если от него отнять сумму его цифр, то, представь себе, тоже получится 2000. —А вот и неправда!— возразила Синеглазка.
Какое число задумала Синеглазка и почему она так ответила Незнайке?

3. Внутри остроугольного треугольника найдите точку, сумма расстояний от которой до всех вершин треугольника и всех его сторон наименьшая.

4. Расшифруйте ребус ТЕТИВА = ИВА². Одинаковым буквам соответствуют одинаковые цифры, разным — разные.

5. Имеется набор из 19 гирек с массами 1 г, 2 г, ..., 19 г. Девять из них железные, ещёдевять — бронзовые, одна — золотая. Сумма масс железных гирек отличается от суммы масс бронзовых гирек на 90 г. Какова масса золотой гирьки?

Задачи третьего номера 1999 года

1. На столе лежала горсть конфет. Первый мальчик взял десятую часть всех конфет. Второй взял десятую часть того, что осталось, и ещё десятую часть того, что взял первый. Третий взял десятую часть того, что осталось, и ещё десятую часть того, что взяли первые двое. Четвёртый взял десятую часть того, что осталось, и ещё десятую часть того, что взяли первые трое... Так продолжалось до тех пор, пока конфеты не кончились. Сколько было мальчиков, и кому из них досталось больше всех конфет?

2. Бабушка хочет поставить на край круглого стола кастрюлю так, чтобы она только на ¹/₃площади своего дна соприкасалась с поверхностью стола. Дедушка утверждает, что в этом случае кастрюля на столе не удержится. Прав ли дедушка?

3. Все натуральные числа от 1 до 100 записаны подряд. Какие-то 25 из них вычеркнули. Можно ли вычеркнуть ещё 25 чисел так, чтобы сумма всех 50 вычеркнутых чисел равнялась сумме всех 50 невычеркнутых?

4. Шерлок Холмс обнаружил начальный обрывок зашифрованного послания, написанного неизвестным ему шифром:

ШЫР-ПИР Ю ПЯПЮЖГЫ ЗЭЛЭМЪГЫЙ ГЁСРЫГ ...

Помогите Холмсу расшифровать сообщение.

Ответ

5. Каждый житель некоторого царства мог быть либо рыцарем, либо лжецом. Рыцари обычно говорят правду. Когда какой-нибудь рыцарь произносит ложь, он тут же погибает. Лжецы обычно говорят неправду. Если какой-то лжец произносит правду, то с этого момента он становится рыцарем. Однажды царь сообщил одному из своих придворных фразу, которая, передаваясь из уст в уста, погубила почти всё населениецарства — уцелел один лишь царь. Докажите, что в этом царстве был по крайней мере один лжец.

Решение

Задачи четвёртого номера 1999 года

1. Балда договорился с попом отработать на него ровно год и расплатиться щелчками по лбу. Он предложил, чтобы за каждый отработанный день ему добавлялся один щелчок, а за каждый прогул вычиталось 10 щелчков. Поп же настаивал на более хитром, по его мнению, варианте: за отработанный день начисляется 12 щелчков, а за пропущенный вычитается аж 121 щелчок. По окончании срока выяснилось, что в обоих случаях поп должен получить от Балды одно и то же число щелчков. Сколько же именно?

2. Шестизначный номер своего телефона я обычно записываю, разбивая цифры на пары и ставя между ними чёрточку. Эти двузначные числа в номере идут в порядке убывания, а их произведение равно двузначному числу, обе цифры которого равны х, причём цифры x в номере нет, но среди цифр имеются четыре последовательные цифры. Какой у меня номер телефона?

3. В противоположных углах квадратной комнаты положили два одинаковых прямоугольных ковра, каждый из которых двумя своими сторонами примыкает к стенам комнаты. Площадь их общей части оказалась равна a. Затем один из ковров развернули в своём углу на 90 градусов. Площадь общей части стала равна b. На сколько длина ковра больше ширины?

4. 9 горизонтальных и 9 вертикальных прямых разрезали квадрат на 100 прямоугольников. Среди них оказалось в точности 9 квадратов. Докажите, что среди квадратов найдутся 2 равных.

5. 16 карточек занумеровали от 1 до 16. Можно ли их выложить вдоль одной прямой так, чтобы сумма номеров любых двух соседних карточек была квадратом?

Задачи пятого номера 1999 года

1. Даны две деревянные палочки. Разрешено прикладывать их одну к другой и делать засечки на любой из них. Как узнать, что больше: длина первой палочки или две трети длины второй?

2. 5 вершин правильного 110-угольника покрасили в красный цвет, a 11 еговершин — в синий цвет так, что красные точки являются вершинами правильного 5-угольника, а синие — вершинами правильного 11-угольника.Докажите, что у 110-угольника есть сторона, концы которой окрашены в красный и синий цвета.

3. В ознаменование окончания учебного года Миша решил вырвать из своего учебника математики все листы, сумма номеров страниц на обеих сторонах каждого из которых является квадратом целого числа, а Гриша собрался удалить все листы, для которых эта сумма является кубом целого числа. Кто из них нанесёт учебнику больший ущерб?

4. а) Существует ли развёртка куба 1×1×1, четырьмя экземплярами которой можно оклеить куб 2×2×2?
б) А такая, двумя экземплярами которой можно оклеить куб, площадь каждой из граней которого равна 2?

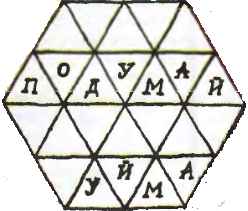5. Расставьте в пустые треугольные ячейки шестиугольника буквы П, О, Д, У, М, А, Й так, чтобы ни в одной полоске каждого из трёх направлений не было одинаковых букв.

Задачи шестого номера 1999 года

1. Расшифруйте числовой ребус БEEE + Б = МУУУ. Одинаковым буквам соответствуют одинаковые цифры, разным — разные.

2. Можно ли расставить в клетках квадрата 4×4 числа от 1 до 16 так, чтобы в каждой клетке стояло число или меньшее всех своих соседей по сторонам, или большее всех своих соседей?

3. «Квадрат или не квадрат?»— рассуждал Лягушонок, разглядывая выражение

11 111 112 222 222 – 3 333 333.

А вы что думаете?

4. На планете Куб (разумеется, имеющей форму куба) каждой гранью владеет правдолюб (который всегда говорит правду) или лжец (который всегда врет). Каждый из них утверждает, что не менее трёх из его соседей — лжецы. Сколько правдолюбов и сколько лжецов владеют гранями планеты?

5. Шестнадцать точек расположены в узлах квадратной решетки. Раскрасьте их в два цвета, чтобы не оказалось прямоугольников с одинаково окрашенными вершинами.